题目内容
用反证法证明命题“设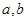
为实数，则方程
至少有一个实根”时，要做的假设是（ ）
| A．方程没有实根 | B．方程至多有一个实根 |
| C．方程至多有两个实根 | D．方程恰好有两个实根 |
解析
练习册系列答案
相关题目
某算法的程序框图如图所示,其中输入的变量x在1,2,3,…,24这24个整数中等可能随机产生.
(1)分别求出按程序框图正确编程运行时输出y的值为i的概率Pi(i=1,2,3);
(2)甲、乙两同学依据自己对程序框图的理解,各自编写程序重复运行n次后,统计记录了输出y的值为i(i=1,2,3)的频数.以下是甲、乙所作频数统计表的部分数据.
甲的频数统计表(部分)
| 运行 次数n | 输出y的值 为1的频数 | 输出y的值 为2的频数 | 输出y的值 为3的频数 |
| 30 | 14 | 6 | 10 |
| … | … | … | … |
| 2100 | 1027 | 376 | 697 |
| 运行 次数n | 输出y的值 为1的频数 | 输出y的值 为2的频数 | 输出y的值 为3的频数 |
| 30 | 12 | 11 | 7 |
| … | … | … | … |
| 2100 | 1051 | 696 | 353 |
用反证法证明命题：“若整系数一元二次方程
有有理根，那么
中至少有一个是偶数时，下列假设中正确的是
| A．假设都是偶数 |
| B．假设都不是偶数 |
| C．假设至多有一个是偶数 |
| D．假设至多有两个是偶数 |
用反证法证明命题：“若a，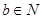
，
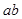能被5整除，则a，b中至少有一个能被5整除”，那么假设的内容是( )
| A．a，b都能被5整除 | B．a，b都不能被5整除 |
| C．a，b有一个能被5整除 | D．a，b有一个不能被5整除 |
已知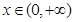
有下列各式：
，
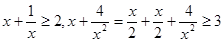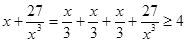成立，观察上面各式，按此规律若
，则正数
( )
| A．4 | B．5 | C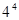． | D． |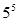
用数学归纳法证明1＋
＋
＋…＋
>
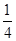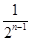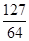(n∈N*)成立，其初始值至少应取( )
| A．7 | B．8 | C．9 | D．10 |
若P＝
＋
，Q＝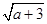
＋
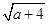(a≥0)，则P，Q的大小关系( )
| A．P>Q | B．P＝Q |
| C．P<Q | D．由a取值决定 |
用数学归纳法证明1＋2＋3＋…＋(2n＋1)＝(n＋1)(2n＋1)时，从n＝k到n＝k＋1，左边需增添的代数式是( )
| A．2k＋2 | B．2k＋3 |
| C．2k＋1 | D．(2k＋2)＋(2k＋3) |