题目内容
设正四棱锥的侧棱与底面所成的角为α，侧面与底面所成的角为β，则tanβ：tanα的值是（ ）
分析：先在正四棱锥得到侧棱与底面所成的角α以及侧面与底面所成的角β；然后根据下底面正方形内长度之间的关系即可求出结论．
解答：
解：设下底面正方形边长为a；
过点P做PO垂直下底面于O，
则O为下底面中心
则∠PBO即为侧棱与底面所成的角α，
取BC中点E，连接PE，OE；
由正四棱锥的侧面都是等腰三角形可得：PE⊥BC，
因为PO垂直下底面于O
则∠PEO即为侧面与底面所成的角β，
在正四面体中，tanα=
tanβ=
．
∴tanβ：tanα=
=
=
=
：1．
故选：B．
解：设下底面正方形边长为a；过点P做PO垂直下底面于O，
则O为下底面中心
则∠PBO即为侧棱与底面所成的角α，
取BC中点E，连接PE，OE；
由正四棱锥的侧面都是等腰三角形可得：PE⊥BC，
因为PO垂直下底面于O
则∠PEO即为侧面与底面所成的角β，
在正四面体中，tanα=
| PO |
| OB |
tanβ=
| PO |
| OE |
∴tanβ：tanα=
| OB |
| OE |
| ||||
|
| 2 |
| 2 |
故选：B．
点评：本小题主要考查空间线面关系、二面角的度量等知识，考查数形结合、化归与转化的数学思想方法，以及空间想象能力、推理论证能力和运算求解能力．解决本题的关键在于做出角α以及角β．
练习册系列答案
相关题目
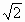，底面边长为
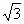，E是SA的中点，则异面直线BE与SC所成的角是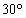
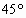
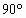
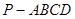中，
．
；
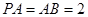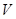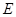为侧棱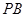
的中点，求异面直线
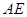与
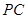
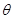的大小．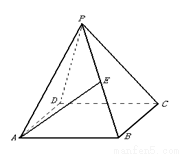
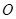为底面正方形
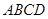中心，则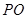
为该正四棱锥的高由已知，可求得
，
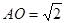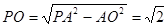
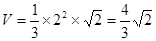
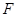为
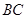中点，连结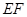
、
，
，
，
，
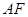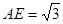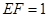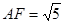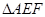中，由余弦定理，得
．
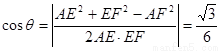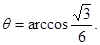
,侧面与底面所成的角为
,则
:
的值是（ ） 
:1 C. 
:
D.