题目内容
 在正方体ABCD-A1B1C1D1中,P、M、N分别为棱DD1、AB、BC的中点.
在正方体ABCD-A1B1C1D1中,P、M、N分别为棱DD1、AB、BC的中点.(1)求二面角B1-MN-B的正切值;
(2)画出一个正方体的表面展开图,使其满足“有4个正方形相连成一个长方形”这一条件,并求展开图中P、B两点间的距离(设正方体的棱长为1).
分析:(1)要求二面角B1-MN-B的正切值,我们要先找出二面角的平面角,再构造三角形,解三角形求出其正切值.
(2)由正方体12种展开图,选其中“1-4-1”的情况,再标识出P点即可,从而可求PB.
(2)由正方体12种展开图,选其中“1-4-1”的情况,再标识出P点即可,从而可求PB.
解答: 解:(1)连接BD交MN于F,则BF⊥MN,连接B1F.
解:(1)连接BD交MN于F,则BF⊥MN,连接B1F.
∵B1B⊥平面ABCD,∴B1B⊥MN.
又∵BD⊥MN,B1B∩BD=B,∴MN⊥平面B1BF
∴MN⊥B1F,∴∠B1FB为二面角B1-MN-B的平面角.
在Rt△B1BF中,B1B=1,BF=
,∴tan∠B1FB=2
;
(2)符合条件的正方体表面展开图可以是以下6种情况之一.
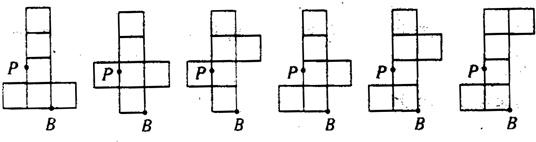
由图可知PB=
=
 解:(1)连接BD交MN于F,则BF⊥MN,连接B1F.
解:(1)连接BD交MN于F,则BF⊥MN,连接B1F.∵B1B⊥平面ABCD,∴B1B⊥MN.
又∵BD⊥MN,B1B∩BD=B,∴MN⊥平面B1BF
∴MN⊥B1F,∴∠B1FB为二面角B1-MN-B的平面角.
在Rt△B1BF中,B1B=1,BF=
| ||
| 4 |
| 2 |
(2)符合条件的正方体表面展开图可以是以下6种情况之一.

由图可知PB=
1+(
|
| ||
| 2 |
点评:本题考查线面角,考查展开图,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
 16、在正方体ABCD-A′B′C′D′中,过对角线BD′的一个平面交AA′于E,交CC′于F,则
16、在正方体ABCD-A′B′C′D′中,过对角线BD′的一个平面交AA′于E,交CC′于F,则
 如图,在正方体ABCD-A′B′C′D′中,E,F分别是AB′,BC′的中点.
如图,在正方体ABCD-A′B′C′D′中,E,F分别是AB′,BC′的中点.  如图在正方体ABCD-A 1B1C1D1中,O是底面ABCD的中心,B1H⊥D1O,H为垂足,则B1H与平面AD1C的位置关系是( )
如图在正方体ABCD-A 1B1C1D1中,O是底面ABCD的中心,B1H⊥D1O,H为垂足,则B1H与平面AD1C的位置关系是( )