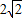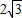题目内容
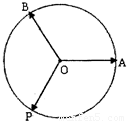
点M是单位圆O(O是坐标原点)与X轴正半轴的交点,点P在单位圆上,∠MOP=x,OQ=OP=OM,四边形OMQP的面积为S,函数f(x)=OM•OQ+
S.求函数f(x)的表达式及单调递增区间.
| 3 |
分析:由题设条件知M(1,0),P(cosx,sinx),故
=(1+cosx,sinx),
•
=1+cosx,S=sinx,由此能求出函数f(x)的表达式及单调递增区间.
| OQ |
| OM |
| OQ |
解答:解:∵点M是单位圆O(O是坐标原点)与X轴正半轴的交点,
∴M(1,0),
∵点P在单位圆上,∠MOP=x,OQ=OP=OM,
∴P(cosx,sinx),
∴
=(1+cosx,sinx),
•
=1+cosx,
∵S=sinx,
∴f(x)=1+cosx+
sinx=2sin(x+
)+1,0<x<π,
令-
+2kπ≤x+
≤
+2kπ,
∴-
+2kπ≤x≤
+2kπ,k∈Z.
∵0<x<π,
∴函数f(x)的单递增调区间为(0,
].
∴M(1,0),
∵点P在单位圆上,∠MOP=x,OQ=OP=OM,
∴P(cosx,sinx),
∴
| OQ |
| OM |
| OQ |
∵S=sinx,
∴f(x)=1+cosx+
| 3 |
| π |
| 6 |
令-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
∴-
| 2π |
| 3 |
| π |
| 3 |
∵0<x<π,
∴函数f(x)的单递增调区间为(0,
| π |
| 3 |
点评:本题考查函数f(x)的表达式及单调递增区间的求法,解题时要认真审题,仔细解答,注意单位圆及三角函数知识的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
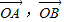 是两个给定的夹角为120°的向量,P为单位圆上一动点,设
是两个给定的夹角为120°的向量,P为单位圆上一动点,设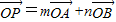 ,则设m+n的最大值为M,最小值为N,则M-N的值为( )
,则设m+n的最大值为M,最小值为N,则M-N的值为( )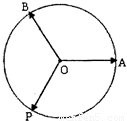
 是两个给定的夹角为120°的向量,P为单位圆上一动点,设
是两个给定的夹角为120°的向量,P为单位圆上一动点,设 ,则设m+n的最大值为M,最小值为N,则M-N的值为( )
,则设m+n的最大值为M,最小值为N,则M-N的值为( )


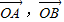 是两个给定的夹角为120°的向量,P为单位圆上一动点,设
是两个给定的夹角为120°的向量,P为单位圆上一动点,设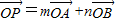 ,则设m+n的最大值为M,最小值为N,则M-N的值为( )
,则设m+n的最大值为M,最小值为N,则M-N的值为( )