题目内容
 二次函数f(x)的部分图象如图,则|f(x)|≤2的解集为
二次函数f(x)的部分图象如图,则|f(x)|≤2的解集为[3-
,2]∪[4,3+
]
| 5 |
| 5 |
[3-
,2]∪[4,3+
]
.| 5 |
| 5 |
分析:由已知中函数的图象以(3,3)为顶点开口朝下且经过(5,-1)点,我们可以求出函数的解析式,进而可根据绝对值的性质可以将不等式|f(x)|≤2化为一个一元二次不等式组,进而得到答案.
解答:解:由已知可得函数的图象是以(3,3)为顶点,
经过(5,-1)点且开口朝下的抛物线
故可设f(x)=a(x-3)2+3(a<0)
将x=5,f(x)=-1代入得:a=-1
故f(x)=-(x-3)2+3
故|f(x)|≤2可化为|-(x-3)2+3|≤2
解得3-
≤x≤2,或4≤x≤3+
,
故答案为:[3-
,2]∪[4,3+
]
经过(5,-1)点且开口朝下的抛物线
故可设f(x)=a(x-3)2+3(a<0)
将x=5,f(x)=-1代入得:a=-1
故f(x)=-(x-3)2+3
故|f(x)|≤2可化为|-(x-3)2+3|≤2
解得3-
| 5 |
| 5 |
故答案为:[3-
| 5 |
| 5 |
点评:本题考查的知识点是二次函数的图象,一元二次不等式的解法,其中根据已知中的函数图象求出函数的解析式是解答本题的关键.

练习册系列答案
相关题目

 如图所示:图1是定义在R上的二次函数f(x)的部分图象,图2是函数g(x)=loga(x+b)的部分图象.分别求出函数f(x)和g(x)的解析式.
如图所示:图1是定义在R上的二次函数f(x)的部分图象,图2是函数g(x)=loga(x+b)的部分图象.分别求出函数f(x)和g(x)的解析式. (2011•南通模拟)
(2011•南通模拟)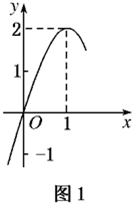 如图所示:图1是定义在R上的二次函数f(x)的部分图象,图2是函数g(x)=loga(x+b)的部分图象.
如图所示:图1是定义在R上的二次函数f(x)的部分图象,图2是函数g(x)=loga(x+b)的部分图象.


 如图所示:图1是定义在R上的二次函数f(x)的部分图象,图2是函数g(x)=loga(x+b)的部分图象.
如图所示:图1是定义在R上的二次函数f(x)的部分图象,图2是函数g(x)=loga(x+b)的部分图象.