题目内容
已知![]()
(1)当![]() 时,求证f(x)在(-1,1)内是减函数;
时,求证f(x)在(-1,1)内是减函数;
(2)若y=f(x)在(-1,1)内有且只有一个极值点,求a的取值范围
解(1):![]() ∴
∴![]()
![]() ∴
∴![]() 且
且![]()
又因为二次函数![]() 的图象开口向上,所以在(-1,1)内
的图象开口向上,所以在(-1,1)内![]() <0,故发
<0,故发![]() 在
在
(-1,1)内为减函数。
(2)设极值点为![]() ,则
,则![]()
当![]() 时,由
时,由![]() ,所以在
,所以在![]() 内
内![]()
在![]() 内
内![]() 即
即![]() 在
在![]() 内递增,
内递增,![]() 在
在![]() 内递减。
内递减。![]() 当
当![]() 时,
时,![]() 在(-1,1)内有且只有一个极值点,且是极大值点;
在(-1,1)内有且只有一个极值点,且是极大值点;![]() 时,同理可知,
时,同理可知,![]() 在(-1,1)内有且只有一个极值点,且是极小值点。
在(-1,1)内有且只有一个极值点,且是极小值点。
当![]() 时,由(1)知
时,由(1)知![]() 在(-1,1)内没有极值点。
在(-1,1)内没有极值点。
故![]() 的取值范围是
的取值范围是![]()

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目


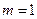 时,求
时,求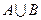 ;
;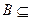
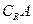 ,求实数
,求实数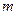 的取值范围.
的取值范围.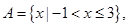
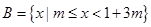
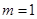 时,求
时,求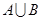 ;
;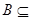
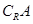 ,求实数
,求实数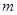 的取值范围.
的取值范围.

 时,求
时,求 ;
;
 ,求实数
,求实数 的取值范围.
的取值范围.