题目内容
1.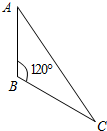 在△ABC中,AB=BC=4,∠ABC=120°,若把△ABC绕直线AB旋转一周,
在△ABC中,AB=BC=4,∠ABC=120°,若把△ABC绕直线AB旋转一周,求所形成的几何体的体积V和表面积S.
分析 如图所示,把△ABC绕直线AB旋转一周,是以AO为底面上的高、OC为半径的大圆锥减去同底面以BO为高的圆锥后剩下的几何体.利用圆锥的体积计算公式与侧面积计算公式即可得出.
解答 解:如图所示,
把△ABC绕直线AB旋转一周,是以AO为底面上的高、OC为半径的大圆锥减去同底面以BO为高的圆锥后剩下的几何体.
∵∠ABC=120°,∴∠OBC=60°.
∵BC=4,∴OB=2,OC=2$\sqrt{3}$.
∴AO=AB+BO=6.
∴V=$\frac{1}{3}π×O{C}^{2}(AO-BO)$=$\frac{1}{3}×π×(2\sqrt{3})^{2}×4$=16π.
∵AC=$\sqrt{A{O}^{2}+O{C}^{2}}$=$\sqrt{{6}^{2}+(2\sqrt{3})^{2}}$=4$\sqrt{3}$.
∴S=S大圆锥侧面积+S小圆锥侧面积
=π•OC•AC+πOC•BC
=$π×2\sqrt{3}×4\sqrt{3}$+$π×2\sqrt{3}×4$
=$(24+8\sqrt{3})$π.
点评 本题考查了旋转体圆锥的体积计算公式与侧面积计算公式、直角三角形的边角关系、勾股定理、圆的面积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
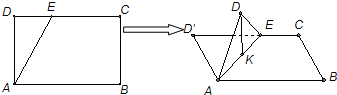
16.如图,在矩形ABCD中,AB=$\sqrt{3}$,BC=1,E为线段CD上一动点,现将△AED沿AE折起,使平面AED⊥平面ABC,当E从D运动到C,则D在平面ABC上的射影K所形成轨迹的长度为( )

| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{3}$ |
6.圆x2+y2+4x-6y-3=0的圆心和半径分别为( )
| A. | (-2,3),4 | B. | (-2,3),16 | C. | (2,-3),4 | D. | (4,-6),16 |
13.sin75°=( )
| A. | $\frac{\sqrt{6}-\sqrt{3}}{4}$ | B. | $\frac{\sqrt{6}+\sqrt{2}}{4}$ | C. | $\frac{\sqrt{6}+\sqrt{3}}{4}$ | D. | $\frac{\sqrt{6}-\sqrt{2}}{4}$ |
10. 如图,在等腰梯形ABDE中,AE=ED=BD=a,当等腰梯形ABDE的面积最大时,角θ为( )
如图,在等腰梯形ABDE中,AE=ED=BD=a,当等腰梯形ABDE的面积最大时,角θ为( )
 如图,在等腰梯形ABDE中,AE=ED=BD=a,当等腰梯形ABDE的面积最大时,角θ为( )
如图,在等腰梯形ABDE中,AE=ED=BD=a,当等腰梯形ABDE的面积最大时,角θ为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{8}$ |