题目内容
设函数f(x)=x2ex-1-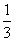 x3-x2(x∈R),
x3-x2(x∈R),
(Ⅰ)求函数y=f(x)的单调区间;
(Ⅱ)求y=f(x)在[-l,2]上的最小值;
(Ⅲ)当x∈(1,+∞)时,用数学归纳法证明: n∈N*,ex-1>
n∈N*,ex-1>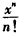 。
。
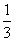 x3-x2(x∈R),
x3-x2(x∈R),(Ⅰ)求函数y=f(x)的单调区间;
(Ⅱ)求y=f(x)在[-l,2]上的最小值;
(Ⅲ)当x∈(1,+∞)时,用数学归纳法证明:
 n∈N*,ex-1>
n∈N*,ex-1>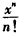 。
。解:(Ⅰ)
 ,
,
令 ,可得
,可得 ,
,

函数y=f(x)的增区间为(-2,0)和(1,+∞),减区间为(-∞,-2)和(0,1)。
(Ⅱ)当 时,
时, ,
, ,
,
 ,
,
所以,f(x)在 上的最小值为
上的最小值为 。
。
(Ⅲ)设 ,
,
当n=1时,只需证明 ,
,
当 时,
时, ,
,
所以, 在
在 上是增函数,
上是增函数,
∴ ,即
,即 ,
,
当 时,假设n=k时不等式成立,
时,假设n=k时不等式成立,
即 ,
,
当n=k+1时,
因此, ,
,
所以, 在
在 上是增函数,
上是增函数,
所以, ,
,
即当n=k+1时,不等式成立,
所以,当 时,
时, 。
。

 ,
,令
 ,可得
,可得 ,
,
函数y=f(x)的增区间为(-2,0)和(1,+∞),减区间为(-∞,-2)和(0,1)。
(Ⅱ)当
 时,
时, ,
, ,
, ,
,所以,f(x)在
 上的最小值为
上的最小值为 。
。(Ⅲ)设
 ,
,当n=1时,只需证明
 ,
,当
 时,
时, ,
,所以,
 在
在 上是增函数,
上是增函数,∴
 ,即
,即 ,
,当
 时,假设n=k时不等式成立,
时,假设n=k时不等式成立,即
 ,
,当n=k+1时,
因此,
 ,
,所以,
 在
在 上是增函数,
上是增函数,所以,
 ,
,即当n=k+1时,不等式成立,
所以,当
 时,
时, 。
。
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 设函数
设函数 设函数
设函数