题目内容
(1)已知f(x)= ,(x∈R,且x≠-1),g(x)=x2+2x,(x∈R),求f(3),f[g(3)]的值.
,(x∈R,且x≠-1),g(x)=x2+2x,(x∈R),求f(3),f[g(3)]的值.
(2)已知f(2x+1)=x2-2x,求f(x)的解析式.
解:(1)∵f(x)= ,g(x)=x2+2x
,g(x)=x2+2x
∴f(3)= ,g(3)=15
,g(3)=15
∴f[g(3)]=f(15)=
(2)令2x+1=t则x=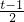
∴f(t)=(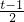 )2-2(
)2-2(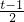 )=
)= t2-
t2- t+
t+
∴f(x)= x2-
x2- x+
x+
分析:(1)由f(x)= ,g(x)=x2+2x可得f(3)=
,g(x)=x2+2x可得f(3)= ,g(3)=15,则f[g(3)]=f(15)代入可求
,g(3)=15,则f[g(3)]=f(15)代入可求
(2)令2x+1=t则x=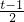 ,利用代入可求f(t),进而可求f(x)
,利用代入可求f(t),进而可求f(x)
点评:本题主要考查了利用代入法求解函数值,及换元法求解函数的解析式,属于基础试题
 ,g(x)=x2+2x
,g(x)=x2+2x∴f(3)=
 ,g(3)=15
,g(3)=15∴f[g(3)]=f(15)=

(2)令2x+1=t则x=
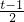
∴f(t)=(
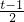 )2-2(
)2-2(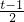 )=
)= t2-
t2- t+
t+
∴f(x)=
 x2-
x2- x+
x+
分析:(1)由f(x)=
 ,g(x)=x2+2x可得f(3)=
,g(x)=x2+2x可得f(3)= ,g(3)=15,则f[g(3)]=f(15)代入可求
,g(3)=15,则f[g(3)]=f(15)代入可求(2)令2x+1=t则x=
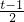 ,利用代入可求f(t),进而可求f(x)
,利用代入可求f(t),进而可求f(x)点评:本题主要考查了利用代入法求解函数值,及换元法求解函数的解析式,属于基础试题

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
已知f(x)的定义域为x∈R且x≠1,已知f(x+1)为奇函数,当x<1时,f(x)=2x2-x+1,那么,当x>1时,f(x)的递减区间是( )
A、[
| ||
B、[1,
| ||
C、[
| ||
D、(1,
|