题目内容
5.已知函数f(x)=$\left\{\begin{array}{l}{3-{x}^{2},x∈[-1,2]}\\{x-3,x∈(2,5]}\end{array}\right.$(1)在给定的直角坐标系内画出f(x)的图象
(2)写出f(x)的单调递增区间与减区间.
分析 (1)结合二次函数和一次函数的图象和性质,及已知中函数的解析式,可得函数的图象;
(2)结合(1)中函数图象,可得函数的单调区间.
解答 解:(1)函数f(x)的图象如下图(6分)
(2)当x∈[-1,2]时,f(x)=3-x2,
知f(x)在[-1,0]上递增;在[0,2]上递减,
又f(x)=x-3在(2,5]上是增函数,
因此函数f(x)的增区间是[-1,0]和(2,5];减区间是[0,2].(12分)
点评 本题考查的知识点是分段函数的应用,函数的单调区间,难度不大,属于基础题.

练习册系列答案
相关题目
16.设抛物线y2=4x的焦点为F,过F作倾角为60°的直线交抛物线于A、B两点(点A在第一象限),与其准线交于点C,则$\frac{{S}_{△AOC}}{{S}_{BOF}}$=( )
| A. | 6 | B. | 7 | C. | 8 | D. | 10 |
10.三个数0.42,20.4,log0.42的大小关系为( )
| A. | 0.42<20.4<log0.42 | B. | log0.42<0.42<20.4 | ||
| C. | 0.42<log0.42<20.4 | D. | log0.42<20.4<0.42 |
17.(Ⅰ)如表所示是某市最近5年个人年平均收入表节选.求y关于x的回归直线方程,并估计第6年此市的个人年平均收入(保留三位有效数字).
其中$\sum_{i=1}^{5}$xiyi=421,$\sum_{i=1}^{5}$xi2=55
附1:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overrightarrow{y}$-$\stackrel{∧}{b}$$\overline{x}$
(Ⅱ)下表是从调查某行业个人平均收入与接受专业培训时间关系得到2×2列联表:
完成上表,并回答:是否有95%以上的把握认为“收入与接受培训时间有关系”.
附2:
附3:
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.(n=a+b+c+d)
| 年份x | 1 | 2 | 3 | 4 | 5 |
| 收入y(千元) | 21 | 24 | 27 | 29 | 31 |
附1:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overrightarrow{y}$-$\stackrel{∧}{b}$$\overline{x}$
(Ⅱ)下表是从调查某行业个人平均收入与接受专业培训时间关系得到2×2列联表:
| 受培时间一年以上 | 受培时间不足一年 | ||
| 收入不低于平均值 | 60 | 20 | |
| 收入低于平均值 | 10 | 10 | |
| 100 |
附2:
| P(K2≥k0) | 0.50 | 0.40 | 0.10 | 0.05 | 0.01 | 0.005 |
| k0 | 0.455 | 0.708 | 2.706 | 3.841 | 6.635 | 7.879 |
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.(n=a+b+c+d)
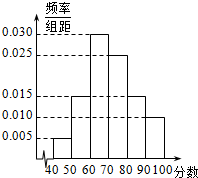 某校高二年级共有学生600名,从某次测试成绩中随机抽出50名同学的成绩,形成样本频率分布直方图如右上,据此估计全年级成绩不少于60分的人数为480.
某校高二年级共有学生600名,从某次测试成绩中随机抽出50名同学的成绩,形成样本频率分布直方图如右上,据此估计全年级成绩不少于60分的人数为480.