题目内容
函数f（x）=
x3-
mx2+4x在[1，3]上是单调增函数，则实数m的取值范围是（ ）A．m≤5
B．m
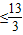
C．m≤4
D．m
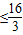
【答案】分析：求函数的导数，利用导数含函数单调性的关系进行判断，要使f（x）在[1，3]上单调增函数，则f'（x）≥0恒成立即可．
解答：解：函数导数为f'（x）=x2-mx+4，要使f（x）在[1，3]上单调增函数，则f'（x）≥0恒成立即可．
即f'（x）=x2-mx+4≥0在[1，3]上恒成立．
即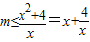
成立．
因为
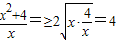，当且仅当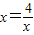
，x=2时取等号，
所以m≤4．
故选C．
点评：本题主要考查函数的单调性和函数单调性之间的关系，将含参问题转化为最值恒成立，是解决本题的关键．
解答：解：函数导数为f'（x）=x2-mx+4，要使f（x）在[1，3]上单调增函数，则f'（x）≥0恒成立即可．
即f'（x）=x2-mx+4≥0在[1，3]上恒成立．
即
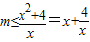成立．因为
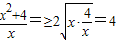，当且仅当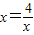，x=2时取等号，所以m≤4．
故选C．
点评：本题主要考查函数的单调性和函数单调性之间的关系，将含参问题转化为最值恒成立，是解决本题的关键．
练习册系列答案
相关题目