题目内容
已知函数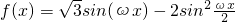 (ω>0)的最小正周期为3π,
(ω>0)的最小正周期为3π,
(Ⅰ)当 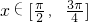 时,求函数f(x)的最小值;
时,求函数f(x)的最小值;
(Ⅱ)在△ABC,若f(C)=1,且2sin2B=cosB+cos(A-C),求sinA的值.
解: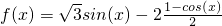 =
=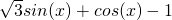 =
=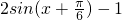
依题意函数f(x)的最小正周期为3π,即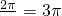 ,解得
,解得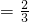 ,
,
所以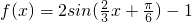
(Ⅰ)由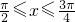 得
得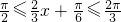 ,
,
所以,当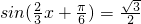 时,
时,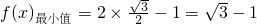
(Ⅱ)由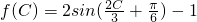 及f(C)=1,得
及f(C)=1,得
而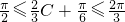 ,所以
,所以 ,解得
,解得
在Rt△ABC中,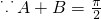 ,2sin2B=cosB+cos(A-C)2cos2A-sinA-sinA=0,
,2sin2B=cosB+cos(A-C)2cos2A-sinA-sinA=0,
∴sin2A+sinA-1=0,解得 ∵0<sinA<1,
∵0<sinA<1,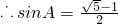
分析:先利用二倍角公式的变形形式及辅助角公式把函数化简为y=2sin(ωx+ )-1,根据周期公式可求ω,进而求f(x)
)-1,根据周期公式可求ω,进而求f(x)
(I)由x的范围求出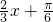 的范围,结合正弦函数的图象及性质可求
的范围,结合正弦函数的图象及性质可求
(II)由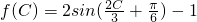 及f(C)=1可得,
及f(C)=1可得, ,结合已知C的范围可求C及 A+B,代入2sin2B=cosB+cos(A-C),整理可得关于 sinA的方程,解方程可得
,结合已知C的范围可求C及 A+B,代入2sin2B=cosB+cos(A-C),整理可得关于 sinA的方程,解方程可得
点评:以三角形为载体,综合考查了二倍角公式的变形形式,辅助角公式在三角函数化简中的应用,考查了三角函数的性质(周期、单调区间、最值取得的条件)时常把ωx+φ作为一个整体.
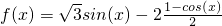 =
=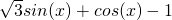 =
=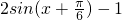
依题意函数f(x)的最小正周期为3π,即
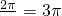 ,解得
,解得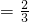 ,
,所以
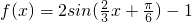
(Ⅰ)由
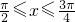 得
得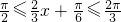 ,
,所以,当
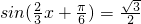 时,
时,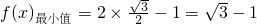
(Ⅱ)由
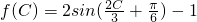 及f(C)=1,得
及f(C)=1,得
而
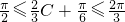 ,所以
,所以 ,解得
,解得
在Rt△ABC中,
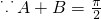 ,2sin2B=cosB+cos(A-C)2cos2A-sinA-sinA=0,
,2sin2B=cosB+cos(A-C)2cos2A-sinA-sinA=0,∴sin2A+sinA-1=0,解得
 ∵0<sinA<1,
∵0<sinA<1,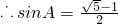
分析:先利用二倍角公式的变形形式及辅助角公式把函数化简为y=2sin(ωx+
 )-1,根据周期公式可求ω,进而求f(x)
)-1,根据周期公式可求ω,进而求f(x)(I)由x的范围求出
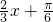 的范围,结合正弦函数的图象及性质可求
的范围,结合正弦函数的图象及性质可求(II)由
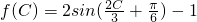 及f(C)=1可得,
及f(C)=1可得, ,结合已知C的范围可求C及 A+B,代入2sin2B=cosB+cos(A-C),整理可得关于 sinA的方程,解方程可得
,结合已知C的范围可求C及 A+B,代入2sin2B=cosB+cos(A-C),整理可得关于 sinA的方程,解方程可得点评:以三角形为载体,综合考查了二倍角公式的变形形式,辅助角公式在三角函数化简中的应用,考查了三角函数的性质(周期、单调区间、最值取得的条件)时常把ωx+φ作为一个整体.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
 (-1≤x≤0)的反函数是( )
(-1≤x≤0)的反函数是( )




 的定义域是 ;
的定义域是 ; 上是减函数,则实数a的取值范围是 .
上是减函数,则实数a的取值范围是 .  终边经过点P(-4,3),求
终边经过点P(-4,3),求 的值?
的值? ,(b>0)在
,(b>0)在 的最大值为
的最大值为 ,最小值为-
,最小值为- ,求2a+b的值?
,求2a+b的值?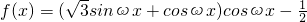 ,(ω>0)的最小正周期为4π.
,(ω>0)的最小正周期为4π. (w>0)的图象的两相邻对称轴间的距离为
(w>0)的图象的两相邻对称轴间的距离为 .
. ,且f(x)=m有且仅有一个实根,求实数m的值.
,且f(x)=m有且仅有一个实根,求实数m的值.