题目内容
已知函数f（x）=3ax+1-2a在[-1，1]上存在零点x0，且x0≠±1，求实数a的取值范围．
解：当a=0时，f（x）=1，此时函数在[-1，1]上不存在零点，所以a≠0．
要使f（x）=3ax+1-2a在[-1，1]上存在零点，且x0≠±1，则有f（-1）f（1）＜0，
即（3a+1-2a）（-3a+1-2a）＜0，所以（a+1）（5a-1）＞0，
解得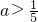
或a＜-1．
分析：利用根的存在定理，可得f（-1）f（1）≤0，求解即可．
点评：本题主要考查函数零点的应用．
要使f（x）=3ax+1-2a在[-1，1]上存在零点，且x0≠±1，则有f（-1）f（1）＜0，
即（3a+1-2a）（-3a+1-2a）＜0，所以（a+1）（5a-1）＞0，
解得
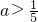或a＜-1．分析：利用根的存在定理，可得f（-1）f（1）≤0，求解即可．
点评：本题主要考查函数零点的应用．
练习册系列答案
考前必练系列答案
相关题目
已知函数f（x）=3•2x-1，则当x∈N时，数列{f（n+1）-f（n）}（ ）
| A、是等比数列 | B、是等差数列 | C、从第2项起是等比数列 | D、是常数列 |