Question

（本小题满分13分）

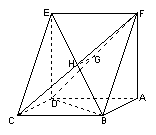
如图，已知平行四边形中，四边形为正方形，平面平面分别是的中点.

（Ⅰ）求证：∥平面

（Ⅱ）记表示四棱锥的体积.

(ⅰ)求的表达式；

（ⅱ）当取得最大值时，求平面与平面所成锐二面角的余弦值.

Answer 1

（Ⅰ）证法１：∵, ∴且

∴四边形EFBC是平行四边形　∴H为FC的中点-------------2分

又∵G是FD的中点

∴---------------------------------------3分

∵平面CDE，平面CDE

∴GH∥平面CDE  ---------------------------------4分

证法２：连结EA，∵ADEF是正方形　　∴G是AE的中点 -------1分

∴在⊿EAB中， ------------------------------------------------------------------2分

又∵AB∥CD，∴GH∥CD，-----------------------------------------------------------------3分

∵平面CDE，平面CDE

∴GH∥平面CDE  ---------------------------------------------------4分

（Ⅱ）∵平面ADEF⊥平面ABCD，交线为AD

且FA⊥AD，　　∴FA⊥平面ABCD.----------------------------------- ---------------6分

∵BD⊥CD, ，  ∴FA=2,（）

∴ ＝            

∴（）- ks*5*u ---------------8分

（Ⅲ）要使取得最大值，只须＝（）取得最大值，

∵，当且仅当即时

取得最大值-----------------------------------------------------------------------9分

解法１：在平面DBC内过点D作于M，连结EM

∵　　∴平面EMD　　∴

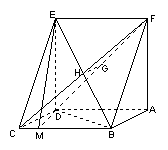∴是平面ECF与平面ABCD所成的二面角的平面角-------12分

∵当取得最大值时，,

∴,

∴

即平面ECF与平面ABCD所成的二面角的余弦值为.------------------------------13分

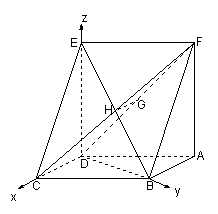解法２：以点D为坐标原点，DC所在的直线为轴，所在的直线为轴，所在的直线为轴建立空间直角坐标系如图示，------9分

则,

∴,,-------10分

设平面ECF与平面ABCD所成的二面角为，

平面ECF的法向量

由得

令得  ------11分

 又∵平面ABCD的法向量为

∴.------------------------13分