题目内容
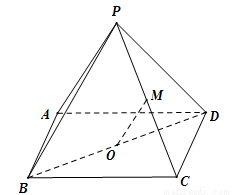
(本小题满分14分)如图,四棱锥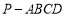 的底面ABCD 是平行四边形,平面PBD⊥平面 ABCD, PB=PD,
的底面ABCD 是平行四边形,平面PBD⊥平面 ABCD, PB=PD, ⊥
⊥ ,
, ⊥
⊥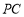 ,
,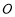 ,
,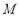 分别是
分别是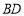 ,
,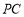 的中点,连结
的中点,连结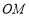 .求证:
.求证:
(1) ∥平面
∥平面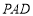 ;
;
(2) ⊥平面
⊥平面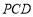 .
.
(1)详见解析(2)详见解析
【解析】
试题分析:(1)证明线面平行,关键证明线线平行,这可根据三角形中位线性质得到:在△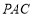 中,因为
中,因为 ,
,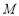 分别是
分别是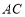 ,
,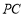 的中点,所以
的中点,所以 ∥
∥ .再根据线面平行判定定理进行证明(2)证明线面垂直,需多次利用线线垂直与线面垂直相互转化:先根据面面垂直性质定理转化为线面垂直:由平面PBD⊥平面ABCD,得
.再根据线面平行判定定理进行证明(2)证明线面垂直,需多次利用线线垂直与线面垂直相互转化:先根据面面垂直性质定理转化为线面垂直:由平面PBD⊥平面ABCD,得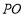 ⊥平面
⊥平面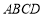 .从而
.从而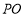 ⊥
⊥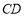 .又因为
.又因为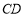 ⊥
⊥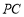 ,所以可得
,所以可得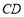 ⊥平面
⊥平面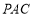 .从而
.从而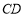 ⊥
⊥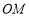 .又因为
.又因为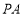 ⊥
⊥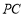 ,
,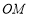 ∥
∥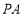 ,所以
,所以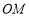 ⊥
⊥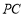 .从而可证
.从而可证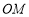 ⊥平面
⊥平面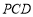 .
.
试题解析:证明:(1)连结AC,
因为ABCD 是平行四边形,所以O为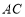 的中点. 2分
的中点. 2分
在△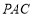 中,因为
中,因为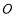 ,
,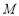 分别是
分别是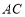 ,
,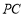 的中点,
的中点,
所以 ∥
∥ . 4分
. 4分
因为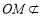 平面
平面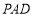 ,
,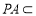 平面
平面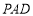 ,
,
所以 ∥平面
∥平面 . 6分
. 6分
(2)连结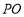 .因为
.因为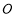 是
是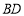 的中点,PB=PD,
的中点,PB=PD,

所以PO⊥BD.
又因为平面PBD⊥平面ABCD,平面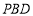
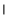 平
平
面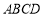 =
=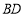 ,
,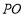
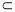 平面
平面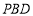
所以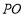 ⊥平面
⊥平面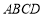 .
.
从而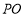 ⊥
⊥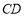 . 8分
. 8分
又因为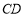 ⊥
⊥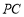 ,
,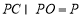 ,
,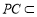 平面
平面 ,
,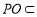 平面
平面 ,
,
所以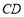 ⊥平面
⊥平面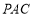 .
.
因为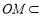 平面
平面 ,所以
,所以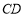 ⊥
⊥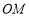 . 10分
. 10分
因为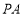 ⊥
⊥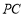 ,
,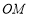 ∥
∥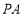 ,所以
,所以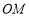 ⊥
⊥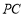 . 12分
. 12分
又因为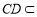 平面
平面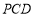 ,
,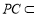 平面
平面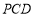 ,
,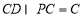 ,
,
所以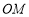 ⊥平面
⊥平面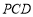 . 14分
. 14分
考点:线面平行判定定理,线面垂直判定定理
考点分析: 考点1:点、线、面之间的位置关系 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
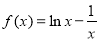 ,
,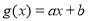 .
.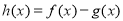 在
在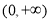 上单调递增,求实数
上单调递增,求实数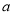 的取值范围;
的取值范围;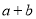 的最小值;
的最小值;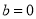 时,若
时,若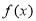 与
与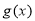 的图象有两个交点
的图象有两个交点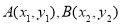 ,求证:
,求证: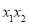
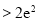 .
.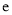 为
为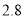 ,取
,取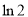 为
为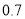 ,取
,取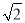 为
为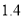 )
)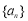 (
(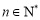 ,
,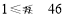 )满足
)满足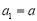 ,
,  其中
其中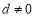 ,
,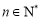 .
.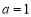 时,求
时,求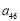 关于
关于 的表达式,并求
的表达式,并求 的取值范围;
的取值范围;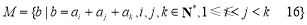 .
.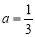 ,
,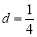 ,求证:
,求证: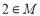 ;
;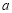 ,
,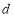 ,使
,使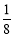 ,
,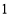 ,
,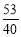 都属于
都属于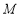 ?若存在,请求出实数
?若存在,请求出实数 (
( ,i为虚数单位),若
,i为虚数单位),若 ,则
,则 的值为 .
的值为 .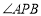 的平分线,
的平分线, 是下半圆的中点.求证:直线PC经过点
是下半圆的中点.求证:直线PC经过点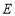 .
.
 ,
, ,设向量
,设向量 满足
满足 ,则
,则 的最大值为 .
的最大值为 . 的定义域为 .
的定义域为 .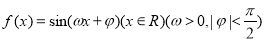 的部分图象如图所示,如果
的部分图象如图所示,如果 ,
,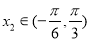 ,且
,且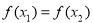 ,则
,则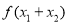 等于( )
等于( )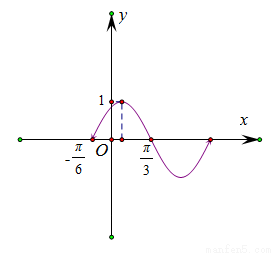
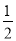 B.
B.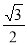 C.
C.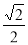 D.
D.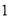
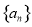 是等差数列,若
是等差数列,若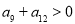 ,
,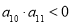 ,且数列
,且数列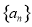 的前
的前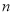 项和
项和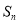 有最大值,那么当
有最大值,那么当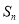 取得最大值时,
取得最大值时,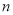 等于 .
等于 .