题目内容
设函数C:f(x)=2ax-
+lnx,若f(x)在x=1,x=-
处取得极值,
(i )求a,b的值;
(ii)在[
,2]存在x0,使得不等式f(x0)-c≤0,求c的最小值.
| b |
| x |
| 1 |
| 2 |
(i )求a,b的值;
(ii)在[
| 1 |
| 4 |
(i)∵f(x)=2ax-
+lnx,定义域为(0,+∞),
∴f′(x)=2a+
+
.
∵f(x)在x=1,x=-
处取得极值,
∴f′(1)=0,f′(
)=0,
即
,
解得:
,
∴所求a,b的值为-
,-
;
(ii)在[
,2]存在存在x0,使得不等式f(x0)-c≤0,只需c≥[f(x)]min,
由f′(x)=-
x-
+
=-
=-
,
∴当x∈[
,
]时,f′(x)<0,故f(x)在[
,
]是单调递减,
当x∈[
,1]时,f′(x)>0,故f(x)在[
,1]是单调递增,
当x∈[1,2]时,f′(x)<0,故f(x)在[1,2]是单调递减;
∴f(
)是f(x)在[
,2]上的极小值,
而f(
)=
+ln
=
-ln2,f(2)=-
+ln2,
且f(
)-f(2)=
-ln4=lne
-ln4,
又e3-16>0,
∴lne
-ln4>0,
∴[f(x)]min=f(2),
∴c≥[f(x)]min=-
+ln2,
∴c的取值范围为[-
+ln2,+∞),
∴c的最小值为
+ln2.
| b |
| x |
∴f′(x)=2a+
| b |
| x2 |
| 1 |
| x |
∵f(x)在x=1,x=-
| 1 |
| 2 |
∴f′(1)=0,f′(
| 1 |
| 2 |
即
|
解得:
|
∴所求a,b的值为-
| 1 |
| 3 |
| 1 |
| 3 |
(ii)在[
| 1 |
| 4 |
由f′(x)=-
| 2 |
| 3 |
| 1 |
| 3x2 |
| 1 |
| x |
| 2x2-3x+1 |
| 3x2 |
| (2x-1)(x-1) |
| 3x2 |
∴当x∈[
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
当x∈[
| 1 |
| 2 |
| 1 |
| 2 |
当x∈[1,2]时,f′(x)<0,故f(x)在[1,2]是单调递减;
∴f(
| 1 |
| 2 |
| 1 |
| 4 |
而f(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 7 |
| 6 |
且f(
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
又e3-16>0,
∴lne
| 3 |
| 2 |
∴[f(x)]min=f(2),
∴c≥[f(x)]min=-
| 7 |
| 6 |
∴c的取值范围为[-
| 7 |
| 6 |
∴c的最小值为
| 7 |
| 6 |

练习册系列答案
相关题目
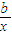 +lnx,若f(x)在x=1,x=-
+lnx,若f(x)在x=1,x=- 处取得极值,
处取得极值, ,2]存在x,使得不等式f(x)-c≤0,求c的最小值.
,2]存在x,使得不等式f(x)-c≤0,求c的最小值.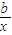 +lnx,若f(x)在x=1,x=-
+lnx,若f(x)在x=1,x=- 处取得极值,
处取得极值, ,2]存在x,使得不等式f(x)-c≤0,求c的最小值.
,2]存在x,使得不等式f(x)-c≤0,求c的最小值.