题目内容
求经过点A(-2,2)且在第二象限与两个坐标轴围成的三角形面积最小时的直线的方程.
x-y+4=0
(解法1)设所求直线方程为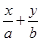 =1(a<0,b>0),
=1(a<0,b>0),
∵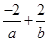 =1,∴a=
=1,∴a=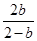 .又a<0,∴b>2.S△=-
.又a<0,∴b>2.S△=-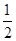 ab=-
ab=-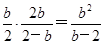 =(b+2)+
=(b+2)+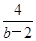 =
=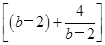 +4≥2
+4≥2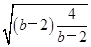 +4=8.当且仅当b-2=
+4=8.当且仅当b-2=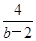 ,即b=4时S最小.此时a=-4,b=4,故x-y+4=0为所求直线方程.
,即b=4时S最小.此时a=-4,b=4,故x-y+4=0为所求直线方程.
(解法2)设所求直线方程为y-2=k(x+2),显然k>0,由题意,S△=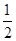 |2k+2|·
|2k+2|·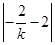 =4+2(k+
=4+2(k+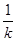 )≥8.当且仅当k=1时取等号,故x-y+4=0为所求直线方程.
)≥8.当且仅当k=1时取等号,故x-y+4=0为所求直线方程.
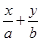 =1(a<0,b>0),
=1(a<0,b>0),∵
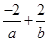 =1,∴a=
=1,∴a=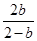 .又a<0,∴b>2.S△=-
.又a<0,∴b>2.S△=-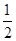 ab=-
ab=-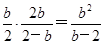 =(b+2)+
=(b+2)+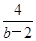 =
=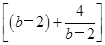 +4≥2
+4≥2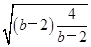 +4=8.当且仅当b-2=
+4=8.当且仅当b-2=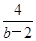 ,即b=4时S最小.此时a=-4,b=4,故x-y+4=0为所求直线方程.
,即b=4时S最小.此时a=-4,b=4,故x-y+4=0为所求直线方程.(解法2)设所求直线方程为y-2=k(x+2),显然k>0,由题意,S△=
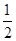 |2k+2|·
|2k+2|·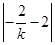 =4+2(k+
=4+2(k+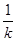 )≥8.当且仅当k=1时取等号,故x-y+4=0为所求直线方程.
)≥8.当且仅当k=1时取等号,故x-y+4=0为所求直线方程.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 并且和
并且和 轴的正半轴、
轴的正半轴、 轴的正半轴所围成的三角形的面积是
轴的正半轴所围成的三角形的面积是 的直线方程.
的直线方程.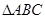 的三个顶点
的三个顶点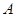 (4,0),
(4,0),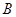 (8,10),
(8,10),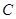 (0,6).
(0,6).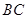 的直线方程;
的直线方程;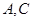 距离相等的直线方程。
距离相等的直线方程。 ,则直线l的方程为________.
,则直线l的方程为________.