题目内容
定义函数f(x)=[x•[x]],其中[x]表示不超过x的最大整数,当x∈[0,n)(n∈N*)时,设函数f(x)的值域为集合A,记A中的元素个数为an,则使 为最小时的n是
为最小时的n是
- A.7
- B.9
- C.10
- D.13
C
分析:由题意易得an,进而可得 =
= ,由函数f(x)=
,由函数f(x)= 的单调性可得答案.
的单调性可得答案.
解答:根据题意:x∈[n-1,n)时,[x]=n-1,
∴x∈[n-1,n)时,[x[x]]=(n-1)2
∴[x[x]]在各区间中的元素个数是:1,2,3,…,n
∴an=1+2=3+…+n= ,∴
,∴ =
= ,
,
构造函数f(x)= ,f′(x)=
,f′(x)= ,
,
令 >0,可得x>
>0,可得x>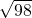 ,
,
故函数f(x)在(1,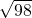 )单调递减,(
)单调递减,(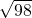 ,+∞)单调递增,
,+∞)单调递增,
故当n=9时, =
= ,当n=10时,
,当n=10时, =
= ,
,
而 ,故当n=10时,
,故当n=10时, 取最小值
取最小值
故选C
点评:本题考查新定义,考查函数的单调性,考查学生分析解决问题的能力,属中档题.
分析:由题意易得an,进而可得
 =
= ,由函数f(x)=
,由函数f(x)= 的单调性可得答案.
的单调性可得答案.解答:根据题意:x∈[n-1,n)时,[x]=n-1,
∴x∈[n-1,n)时,[x[x]]=(n-1)2
∴[x[x]]在各区间中的元素个数是:1,2,3,…,n
∴an=1+2=3+…+n=
 ,∴
,∴ =
= ,
,构造函数f(x)=
 ,f′(x)=
,f′(x)= ,
,令
 >0,可得x>
>0,可得x>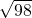 ,
,故函数f(x)在(1,
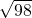 )单调递减,(
)单调递减,(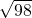 ,+∞)单调递增,
,+∞)单调递增,故当n=9时,
 =
= ,当n=10时,
,当n=10时, =
= ,
,而
 ,故当n=10时,
,故当n=10时, 取最小值
取最小值故选C
点评:本题考查新定义,考查函数的单调性,考查学生分析解决问题的能力,属中档题.

练习册系列答案
相关题目