题目内容
(本小题满分12分)已知![]() ,直线
,直线![]() 与函数
与函数![]() 的图像都相切,且与函数
的图像都相切,且与函数![]() 的图像的切点的横坐标为1。
的图像的切点的横坐标为1。
(I)求直线![]() 的方程及m的值;
的方程及m的值;
(II)若![]() ,求函数
,求函数![]() 的最大值。
的最大值。
(III)当![]() 时,求证:
时,求证:![]()
解:(I)![]()
![]() 的斜率为1,
的斜率为1,
且与函数![]() 的图像的切点坐标为(1,0),
的图像的切点坐标为(1,0),
![]() 的方程为
的方程为![]() …………2分
…………2分
又![]() 与函数
与函数![]() 的图象相切,
的图象相切,
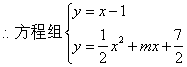 有一解。
有一解。
由上述方程消去y,并整理得![]() ①
①
依题意,方程②有两个相等的实数根,
![]() 解之,
解之,
得m=4或m=-2,![]() …………5分
…………5分
(II)由(I)可知![]()
![]()
![]() …………7分
…………7分
![]() 单调,
单调,
当![]() 时,
时,![]() 单减。
单减。
![]() ,
,![]() 取最大值,其最大值为2。 …………10分
取最大值,其最大值为2。 …………10分
(III)![]() …………11分
…………11分
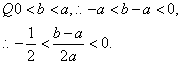
证明,当![]() 时,
时,![]()
![]() …………12分
…………12分

练习册系列答案
 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目