Question

已知f(x)=x²-2x+2,其中x∈［t,t+1］,t∈R.函数f(x)的最小值为t的函数g(t).试计算当t∈［-3,2］时，g(t)的最大值.

Answer 1

解析：由f(x)=x²-2x+2得f(x)=(x-1)²+1图象的对称轴为直线x=1.

    当t+1≤1时，区间［t,t+1］在对称轴的左侧，函数f(x)在x=t+1处取得最小值f(t+1);

    当0＜t＜1时，x=1在区间［t,t+1］的内部，函数f(x)在x=1处取得最小值f(1);

    当t≥1时，区间［t,t+1］在对称轴的右侧，函数f(x)在x=t处取得最小值f（t）.

    综上可得

g(t)=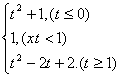

    又t∈［-3,2］,

    当t∈［-3,0］时，求得g(t)的最大值为f(-3)=10;

    当t∈［0,1］时，g(t)恒为1；

    当t∈［1，2］时，求得g(t)的最大值为f(2)=2.

    故当t∈［-3,2］时，g(t)_max=10.