题目内容
已知函数![]() .
.
(Ⅰ)讨论函数![]() 的单调性;
的单调性;
(Ⅱ)设![]() ,证明:对任意
,证明:对任意![]() ,
,![]() .
.
解:(Ⅰ) f(x)的定义域为(0,+![]() ),
),![]() .
.
当a≥0时,![]() >0,故f(x)在(0,+
>0,故f(x)在(0,+![]() )单调增加;
)单调增加;
当a≤-1时,![]() <0, 故f(x)在(0,+
<0, 故f(x)在(0,+![]() )单调减少;
)单调减少;
当-1<a<0时,令![]() =0,解得x=
=0,解得x=![]() .当x∈(0,
.当x∈(0, ![]() )时,
)时, ![]() >0;
>0;
x∈(![]() ,+
,+![]() )时,
)时,![]() <0, 故f(x)在(0,
<0, 故f(x)在(0, ![]() )单调增加,在(
)单调增加,在(![]() ,+
,+![]() )单调减少.
)单调减少.
(Ⅱ)不妨假设x1≥x2.由于a≤-2,故f(x)在(0,+![]() )单调减少.
)单调减少.
所以![]() 等价于
等价于
![]() ≥4x1-4x2,
≥4x1-4x2,
即f(x2)+ 4x2≥f(x1)+ 4x1.
令g(x)=f(x)+4x,则
![]() +4
+4
=![]() .
.
于是![]() ≤
≤![]() =
=![]() ≤0.
≤0.
从而g(x)在(0,+![]() )单调减少,故g(x1) ≤g(x2),
)单调减少,故g(x1) ≤g(x2),
即 f(x1)+ 4x1≤f(x2)+ 4x2,故对任意x1,x2∈(0,+![]() ) ,
) ,![]() .
.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
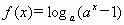 ,(
,(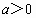 ,
,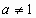 ),
),
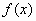 的定义域;
的定义域;
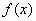 的单调性.
的单调性.