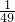Question

某班有五十名学生，其中有五名班干部，现选派三名同学完成某项任务，在班干部甲被选中的条件下干部乙被选中的概率为（　　）

• A．

  1

  49

• B．

  2

  49

• C．

  4

  49

• D．

  6

  49

Answer 1

分析：求出从五十名学生，选派三名同学完成某项任务，班干部甲被选中的种数，以及班干部甲被选中，干部乙被选中的种数，然后后者除以前者即为班干部甲被选中的条件下干部乙被选中的概率．

解答：解：设“班干部甲被选中的条件下干部乙被选中”为事件C，“班干部甲被选中”为事件A，“干部乙被选中”为事件B
从五十名学生，选派三名同学完成某项任务，班干部甲被选中的种数为n（A）=C₄₉²，
从五十名学生，班干部甲被选中，干部乙被选中的种数为n（AB）=C₄₈¹，
∴P（C）=

n(AB)

n(A)

=

48

49×48 2

=

2

49

故选B．

点评：本题考查条件概率的求法，考查学生分析解决问题的能力，属于中档题．