Question

已知集合M={x|y=

2x-x2

}，集合N={y|y=3^x，x＞0}，则如图所示的韦恩图中阴影部分所表示的集合为（　　）

A．（2，+∞）

B．[0，1）∪（2，+∞）

C．[0，1]∪（2，+∞）

D．[0，1]∪[2，+∞）

Answer 1

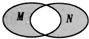
分析：题中韦恩图的含义是在集合M∪N中不在M∩N中，由此解出M∪N和M∩N，再求出集合{x|x∈M∪N且x∉M∩N}，即得本题的答案．

解答：解：M={x|y=

2x-x2

}={x|2x-x2≥0}={x|0≤x≤2}，N={y|y=3^x，x＞0}={y|y＞1}，
则阴影部分为{x|x∈M∪N且x∉M∩N}，M∪N={x|x≥0}，M∩N={x|1＜x≤2}，
所以，即阴影部分为{x|x∈M∪N且x∉M∩N}={x|0≤x≤1或x＞2}，
即[0，1]∪（2，+∞），
故选C．

点评：本题着重考查了韦恩图的认识和集合、函数的定义域和值等基本运算等知识，属于基础题．