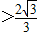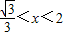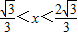Question

长度分别为2、x、x、x、x、x的六条线段能成为同一个四面体的六条棱的充要条件是

 

．

Answer 1

分析：作出四面体的图象，由图象可以判断出度分别为2、x、x、x、x、x的六条线段能成为同一个四面体的六条棱的充要条件是两个面上的中线与相对的棱能组成三角形

解答：解：由图，四面体中BE长为2，其它各边长都是x
取AC中点D，连接DE，DB
由题意B，D，E三点可以构成一个三角形，计算知DE=BD=

3

2

x
故有

3

2

x+

3

2

x＞2，解得x＞

2 3

3

故答案为x＞

2 3

3

点评：本题考查充要条件的判断，求解本题关键是依据图形得出图中的三角形BDE，由三角形的性质得出所要的充要条件．