题目内容
空间图形P—ABC中,∠ABC=90°,PA=1,AB=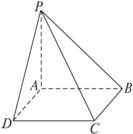
(1)求直线AB与直线PC所成角的正切值;
(2)求直线PC与面ABC所成角的正切值.
解析:(1)作矩形ABCD,则AB与PC所成的角等于CD与PC所成的角∠PCD,
∵PA⊥平面ABC,CD⊥AD,
∴CD⊥面PAD.
∴CD⊥PD.
由CD=![]() ,AC=2得AD=1,
,AC=2得AD=1,
由PA=1,得PD=![]() ,
,
∴tan∠PCD=![]() ,
,
即AB与PC所成角的正切值为![]() .
.
(2)∵PA⊥面ABC,

∴PC与面ABC所成的角为∠ACP.
∴tan∠ACP=![]() ,
,
即直线PC与面ABC所成角的正切值为![]() .
.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目