题目内容
【题目】已知a，b是异面直线，给出下列结论：
①一定存在平面
，使直线
平面，直线
平面；
②一定存在平面，使直线
平面，直线平面；
③一定存在无数个平面，使直线b与平面交于一个定点，且直线平面.
则所有正确结论的序号为（ ）
A.②③B.①③C.①②D.①②③
【答案】A
【解析】
根据异面直线位置关系作出满足条件图形就可证明②③正确，再举例说明①不正确.
因为如果直线
平面
，直线
平面，则必有
，而a，b不一定垂直，所以①不正确；
设
为a，b公垂线段,取中点
,过作
，因为a，b是异面直线，所以
为相交直线，则确定平面，且直线
平面，直线平面；所以②正确；
设为a，b公垂线段, 
，过
作
，过
作平面，使直线b与平面交于一个定点B，则直线平面.此时存在无数个平面，所以③正确；
故选：A
【题目】甲，乙两台机床同时生产一种零件，其质量按测试指标划分：指标大于或等于100为优品，大于等于90且小于100为合格品，小于90为次品，现随机抽取这两台车床生产的零件各100件进行检测，检测结果统计如下：
测试指标 | [85，90） | [90，95） | [95，100） | [100，105） | [105，110） |
机床甲 | 8 | 12 | 40 | 32 | 8 |
机床乙 | 7 | 18 | 40 | 29 | 6 |
（1）试分别估计甲机床、乙机床生产的零件为优品的概率；
（2）甲机床生产一件零件，若是优品可盈利160元，合格品可盈利100元，次品则亏损20元；假设甲机床某天生产50件零件，请估计甲机床该天的日利润（单位：元）；
（3）从甲、乙机床生产的零件指标在[90，95）内的零件中，采用分层抽样的方法抽取5件，从这5件中任选2件进行质量分析，求这2件都是乙机床生产的概率．
【题目】某大型高端制造公司为响应(中国制造2025)中提出的坚持“创新驱动、质量为先、绿色发展、结构优化、人才为本”的基本方针,准备加大产品研发投资,下表是该公司2017年5~12月份研发费用(百万元)和产品销量(万台)的具体数据:
月份 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
研发费用 | 2 | 3 | 6 | 10 | 21 | 13 | 15 | 18 |
产品销量 | 1 | 1 | 2 | 2.5 | 6 | 3.5 | 3.5 | 4.5 |
（1）根据数据可知
与 
之间存在线性相关关系.
(i)求出关于的线性回归方程(系数精确到0.001);
(ii)若2018年6月份研发投人为25百万元，根据所求的线性回归方估计当月产品的销量;
(2)为庆祝该公司9月份成立30周年,特制定以下奖励制度:以
(单位:万台)表示日销量，
,则每位员工每日奖励200元;
,则每位员工每日奖励300元;
,则每位员工每日奖励400元.现已知该公司9月份日销量(万台)服从正态分布
,请你计算每位员工当月(按30天计算)获得奖励金额总数大约多少元
参考数据: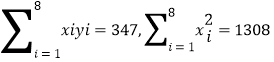
.
参考公式:对于一组数据
.其回归直线
的斜率和截距的最小二乘估计分别为
若随机变量
服从正态分布
,则
.
