Question

(本小题满分12分)

如下图，O₁（– 2，0），O₂（2，0），圆O₁与圆O₂的半径都是1，

 

 

 

 

 

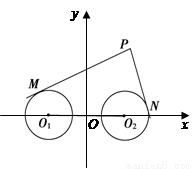
(1)    过动点P分别作圆O₁、圆O₂的切线PM、PN(M、N分别为切点)，使得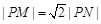．求动点P的轨迹方程；

(2)    若直线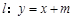交圆O₂于A、B，又点C（3，1），当m取何值时，△ABC的面积最大？

 

Answer 1

【答案】

 

（1）

（2）m = – 1或 – 3

【解析】解：(1) ∵

∴

设P（x，y），则

整理得，即为所求·············································· 6分

        (2) (方法一) ∵

∴ AB∥O₂C

∴ S_△ABC =

(d为O₂到AB的距离)，而

∴

当且仅当时，取等号

而

∴ 时，△O₂AB的面积最大．···························· 12分

   

C到AB的距离

∴

当或– 3时，S取得最大值，而m = – 1，– 3满足①式

∴ m = – 1或 – 3··························································· 12分