题目内容
如图,△ABC中,∠BAC的平分线AD交BC于D,⊙O过点A,且和BC切于D,和AB、AC分别交于E、F.设EF交AD于G,连结DF.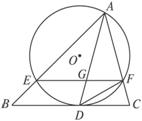
(1)求证:EF∥BC;
(2)已知DF=2,AG=3,求![]() 的值.
的值.
思路解析:由弦切角、圆周角、角平分线,易寻找能使EF∥BC的一对角,再证△ADF∽△FDG,利用相似的性质求比值.
(1)证明:∵⊙O切BC于D,
∴∠CDF=∠DAB.
又∵∠DAB=∠DEF,
∴∠CDF=∠DEF.
∴EF∥BC.
(2)解:∵∠DAB=∠DAC,∠DAB=∠DEF,∴∠DAC=∠DEF.
又∵∠ADF=∠ADF,
∴△ADF∽△FDG.
∴![]() .
.
设GD=x,则![]() .解得x1=1,x2=-4.
.解得x1=1,x2=-4.
经检验x1=1,x2=-4为所列方程的根.
但x2=-4<0应舍去,∴GD=1.
由(1)已证EF∥BC,∴![]() =3.
=3.

练习册系列答案
相关题目
 如图,
如图, 如图,△ABC中,
如图,△ABC中,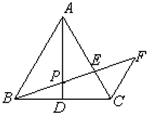 如图,△ABC中,AB=AC,AD是中线,P为AD上一点,CF∥AB,BP延长线交AC、CF于E、F,
如图,△ABC中,AB=AC,AD是中线,P为AD上一点,CF∥AB,BP延长线交AC、CF于E、F, 已知:如图,△ABC中,∠B=60°,AD,CE是角平分线.
已知:如图,△ABC中,∠B=60°,AD,CE是角平分线.