题目内容
△ABC中，角A、B、C所对应的边分别为a、b、c，若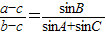
．（1）求角A；
（2）若f（x）=cos2（x+A）-sin2（x-A），求f（x）的单调递增区间．
【答案】分析：（1）由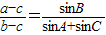
，得
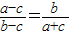，即a2=b2+c2-bc，由余弦定理，得
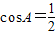，可得A的值．
（2）化简f（x）=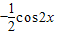
，由 2kπ≤2x≤2kπ+π（k∈Z），求得f（x）的单调递增区间．
解答：解：（1）由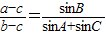
，得
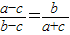，即a2=b2+c2-bc，由余弦定理，得
，
∴
．
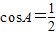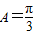（2）f（x）=cos2（x+A）-sin2（x-A）=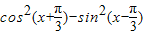
=
=
．
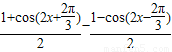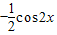由2kπ≤2x≤2kπ+π（k∈Z），得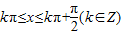
，
故f（x）的单调递增区间为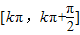
，k∈Z．
点评：本题考查正弦定理、余弦定理的应用，利用余弦函数的单调性，求出角A的值，是解题的关键．
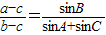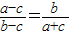，得，即a2=b2+c2-bc，由余弦定理，得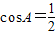，可得A的值．（2）化简f（x）=
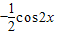，由 2kπ≤2x≤2kπ+π（k∈Z），求得f（x）的单调递增区间．解答：解：（1）由
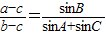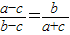，得，即a2=b2+c2-bc，由余弦定理，得，∴
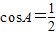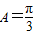．（2）f（x）=cos2（x+A）-sin2（x-A）=
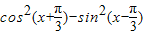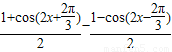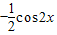==．由2kπ≤2x≤2kπ+π（k∈Z），得
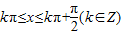，故f（x）的单调递增区间为
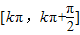，k∈Z．点评：本题考查正弦定理、余弦定理的应用，利用余弦函数的单调性，求出角A的值，是解题的关键．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
相关题目