Question

已知函数y=Msin(ωx+?)，(M＞0，ω＞0，|?|＜

π

2

)的部分图象如图所示，其中B，C为函数的最大值和最小值的对应点，过点B与直线AB：y=x+1垂直的直线BC被圆x²+y²=9所截得的弦长为3

2

．
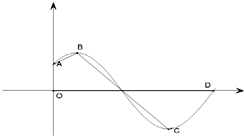
（Ⅰ）求直线BC的方程．
（Ⅱ）求函数y=Msin(ωx+?)，(M＞0，ω＞0，|?|＜

π

2

)的解析式．

Answer 1

分析：（Ⅰ）设出直线BC的方程，利用弦心距、半径、半弦长的关系求出直线BC的方程．
（Ⅱ）求出B 的坐标，BC的方程与x 轴的交点坐标，然后求出函数的周期，利用三角函数经过的特殊点，求出φ，即可求函数y=Msin(ωx+?)，(M＞0，ω＞0，|?|＜

π

2

)的解析式．

解答：解：（I）依题意设直线BC：y=-x+b，…（1分）
圆心O到直线BC的距离d=

9-( 3 2 2 )2

=

3 2

2

，…（3分）
又∵d=

|b|

2

=

3 2

2

，
∴|b|=3，…（5分）
又依题意b＞0，
∴b=3，
∴直线BC：y=-x+3．…（7分）
（II）由

y=x+1 y=-x+3

得：

x=1 y=2

，
∴点B（1，2），
∴M=2．…（8分）
 取直线BC与x轴的交点为E，
∴E（3，0），…（9分）
点B，C关于点E中心对称，
∴C（5，-2）…（10分）
T=2×（5-1）=8，ω＞0，
∴ω=

π

4

∴y=2sin(

π

4

x+?)…（12分）
函数的图象经过点B（1，2），

π

4

+?=2kπ+

π

2

，k∈Z，
∵|φ|＜

π

2

，
∴?=

π

4

，…（13分）
∴y=2sin(

π

4

x+

π

4

)．…（14分）

点评：本题考查三角函数的解析式的求法，直线方程的垂直关系的应用，考查分析问题解决问题的能力．