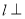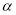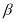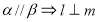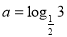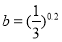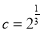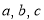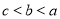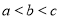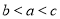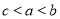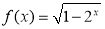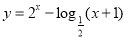题目内容
设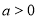 ,
,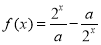 是
是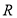 上的奇函数.
上的奇函数.
(Ⅰ)求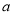 的值;
的值;
(Ⅱ)证明: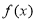 在
在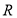 上为增函数;
上为增函数;
(Ⅲ)解不等式: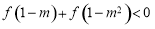 .
.
(Ⅰ) ;(Ⅱ)详见试题详解(Ⅲ)
;(Ⅱ)详见试题详解(Ⅲ)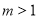 或
或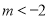
【解析】
试题分析:(1)根据 在R上是奇函数则有
在R上是奇函数则有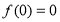 解题(2)根据函数单调性的定义(3)先利用奇偶性把不等式化为两个函数值得大小,再利用单调性得出关于m的一元二次不等式,从而求解
解题(2)根据函数单调性的定义(3)先利用奇偶性把不等式化为两个函数值得大小,再利用单调性得出关于m的一元二次不等式,从而求解
试题解析:(Ⅰ)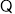
 是
是 上的奇函数.
上的奇函数.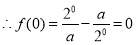 即
即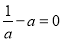 解得
解得
(Ⅱ)由(Ⅰ)知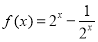 设
设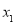 ,
,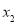 是R上任意两个实数,且
是R上任意两个实数,且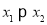


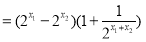
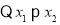
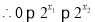
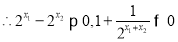

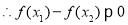 即
即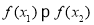 ,
,
所以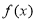 在
在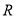 上为增函数;
上为增函数;
(Ⅲ)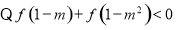
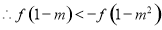
因为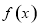 在R上是奇函数所以
在R上是奇函数所以 ,所以
,所以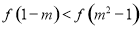 ,
,
因为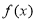 在
在 上为增函数,所以
上为增函数,所以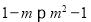
即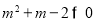 解得
解得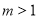 或
或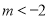
考点:(1)函数的奇偶性(2)函数单调性及其概念

练习册系列答案
相关题目