题目内容

【题目】设0＜a＜1，已知函数f（x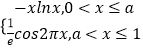）= ，若对任意b∈（0， ），函数g（x）=f（x）﹣b至少有两个零点，则a的取值范围是（ ）
A.
B.
C.
D.

【答案】D
【解析】解：∵f（x）= ，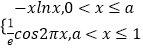
∴f′（x）= ，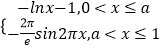
若a＜ ，则当x=a时，函数取极大值f（a）=﹣alna＜ ，
当b∈（﹣alna， ）时，函数g（x）=f（x）﹣b有且只有一个零点，
故a≥ ，
令f（x）=0，x∈（0，1]，则x= ，
故 ∈（a，1]，即a≤ ，
综上可得：a∈ ，
故选：D
【考点精析】解答此题的关键在于理解函数的极值与导数的相关知识，掌握求函数的极值的方法是:（1）如果在附近的左侧,右侧,那么是极大值（2）如果在附近的左侧,右侧,那么是极小值．

练习册系列答案
相关题目

【题目】已知函数在区间上有最大值和最小值.

（1）求的值；

（2）设，

证明：对任意实数，函数的图象与直线最多只有一个交点；

（3）设，是否存在实数m和nm＜n，使的定义域和值域分别为，如果存在，求出m和n的值．若不存在，请说明理由。

【题目】设函数f（x）在R上存在导数f′（x），对任意的x∈R，有f（﹣x）+f（x）=x2 ， 且x∈（0，+∞）时，f′（x）＞x．若f（2﹣a）﹣f（a）≥2﹣2a，则实数a的取值范围为（ ）
A.[1，+∞）
B.（﹣∞，1]
C.（﹣∞，2]
D.[2，+∞）

【题目】设f（x）=sin（ x﹣ ）﹣2cos2 x+1．
（1）求f（x）的最小正周期；
（2）若函数y=f（x）与y=g（x）的图象关于直线x=1对称，求当x∈[0， ]时，y=g（x）的最大值．

【题目】已知函数f（x）= ．
（Ⅰ）若a=﹣1，证明：函数f（x）是（0，+∞）上的减函数；
（Ⅱ）若曲线y=f（x）在点（1，f（1））处的切线与直线x﹣y=0平行，求a的值；
（Ⅲ）若x＞0，证明： （其中e=2.71828…是自然对数的底数）．

【题目】给出以下四个命题：

①若ab≤0，则a≤0或b≤0；②若a>b，则am2>bm2；③在△ABC中，若sinA＝sinB，则A＝B；④在一元二次方程ax2＋bx＋c＝0中，若b2－4ac<0，则方程有实数根.其中原命题、逆命题、否命题、逆否命题全都是真命题的是(　　)

A. ① B. ② C. ③ D. ④

【题目】设函数f（x）=ex ， g（x）=kx+1．
（I）求函数y=f（x）﹣（x+1）的最小值；
（II）证明：当k＞1时，存在x0＞0，使对于任意x∈（0，x0）都有f（x）＜g（x）；
（III）若存在实数m使对任意x∈（0，m）都有|f（x）﹣g（x）|＞x成立，求实数k的取值范围．

【题目】已知函数．

（1）证明：；

（2）若对任意，不等式恒成立，求实数的取值范围．

【题目】如图，DE是⊙O的直径，过⊙O上的点C作直线AB，交ED的延长线于点B，且OA=OB，CA=CB，连结EC，CD．

（1）求证：直线AB是⊙O的切线；
（2）若tan∠CED= ，⊙O的半径为3，求OA的长．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网