题目内容
 在社会实践中,小明观察一棵桃树.他在点A处发现桃树顶端点C的仰角大小为45°,往正前方走4米后,在点B处发现桃树顶端点C的仰角大小为75°.
在社会实践中,小明观察一棵桃树.他在点A处发现桃树顶端点C的仰角大小为45°,往正前方走4米后,在点B处发现桃树顶端点C的仰角大小为75°.
(1)求BC的长;
(2)若小明身高为1.70米,求这棵桃树顶端点C离地面的高度(精确到0.01米,其中 ).
).
解:(1)在△ABC 中,∠CAB=45°,又∠DBC=75°则∠ACB=75°-45°=30°
由正弦定理得到, ,将 AB=4 代入上式,
,将 AB=4 代入上式,
得到 BC=4 (米)
(米)
(2)在△CBD中,∠CDB=90°,BC=4 ,所以DC=4
,所以DC=4 sin75°,
sin75°,
因为sin75°=sin(45°+30°)=sin45°cos30°+cos45°sin30°=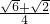 ,
,
则DC=2+2 ,所以DE=
,所以DE= ≈3.70+3.464≈7.16米.
≈3.70+3.464≈7.16米.
答:BC的长4 米;这棵桃树顶端点C离地面的高度7.16米.
米;这棵桃树顶端点C离地面的高度7.16米.
分析:(1)求出∠ACB,利用正弦定理直接求出BC即可.
(2)通过直角三角形,利用两角和的正弦函数求出sin75°,然后求出这棵桃树顶端点C离地面的高度.
点评:本题考查正弦定理,两角和的正弦函数,三角形的求法,考查计算能力.
由正弦定理得到,
 ,将 AB=4 代入上式,
,将 AB=4 代入上式,得到 BC=4
 (米)
(米)(2)在△CBD中,∠CDB=90°,BC=4
 ,所以DC=4
,所以DC=4 sin75°,
sin75°,因为sin75°=sin(45°+30°)=sin45°cos30°+cos45°sin30°=
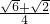 ,
,则DC=2+2
 ,所以DE=
,所以DE= ≈3.70+3.464≈7.16米.
≈3.70+3.464≈7.16米.答:BC的长4
 米;这棵桃树顶端点C离地面的高度7.16米.
米;这棵桃树顶端点C离地面的高度7.16米.分析:(1)求出∠ACB,利用正弦定理直接求出BC即可.
(2)通过直角三角形,利用两角和的正弦函数求出sin75°,然后求出这棵桃树顶端点C离地面的高度.
点评:本题考查正弦定理,两角和的正弦函数,三角形的求法,考查计算能力.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
 在社会实践中,小明观察一棵桃树.他在点A处发现桃树顶端点C的仰角大小为45°,往正前方走4米后,在点B处发现桃树顶端点C的仰角大小为75°.
在社会实践中,小明观察一棵桃树.他在点A处发现桃树顶端点C的仰角大小为45°,往正前方走4米后,在点B处发现桃树顶端点C的仰角大小为75°. ,往正前方走4米后,在点B处发现桃树顶端点C的仰角大小为
,往正前方走4米后,在点B处发现桃树顶端点C的仰角大小为 .
.
 ).
). ).
).
 ).
).