题目内容
已知函数f(x)=
,若f(3-a2)<f(2a),则实数a的取值范围是 .
|
分析:根据分段函数的解析式判断出函数的单调性,利用函数的单调性去掉“f”,转化为关于a的不等式,求解即可得到a的取值范围.
解答:解: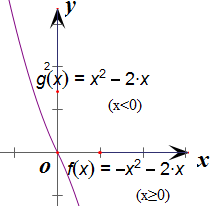 ∵函数f(x)=
∵函数f(x)=
,
作出分段函数的图象如图所示,
∴根据函数的图象可得,函数f(x)在定义域R上是单调递减函数,
∵f(3-a2)<f(2a),
∴3-a2>2a,即a2+2a-3<0,
∴-3<a<1,
实数a的取值范围是-3<a<1.
故答案为:-3<a<1.
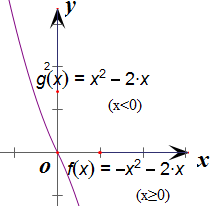 ∵函数f(x)=
∵函数f(x)=
|
作出分段函数的图象如图所示,
∴根据函数的图象可得,函数f(x)在定义域R上是单调递减函数,
∵f(3-a2)<f(2a),
∴3-a2>2a,即a2+2a-3<0,
∴-3<a<1,
实数a的取值范围是-3<a<1.
故答案为:-3<a<1.
点评:本题考查了分段函数的图象,对于分段函数的问题,一般选用分类讨论和数形结合的思想方法进行求解.利用基本初等函数的单调性判断函数的单调性,运用了函数的单调性解不等式,解题的关键是将不等式进行合理的转化,然后利用单调性去掉“f”.属于中档题.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
 已知函数f(x)=
已知函数f(x)=
|
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、[
|