题目内容
在等差数列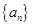 中,
中, ,
, ,则数列
,则数列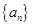 的前
的前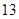 项和为 ( )
项和为 ( )
A.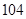 | B. | C.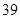 | D. |
B
解析试题分析:由在等差数列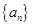 中,又
中,又 即
即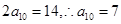 .因为
.因为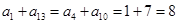 所以数列
所以数列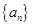 的前
的前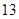 项和为
项和为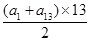 =
=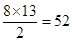 .故选B.本小题关键是通过等差数列的性质进行化简,同样也可以化为首项和公差通过方程组的思想来解决.
.故选B.本小题关键是通过等差数列的性质进行化简,同样也可以化为首项和公差通过方程组的思想来解决.
考点:1.等差数列的性质.2.等差数列的求和公式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在等差数列 中,若
中,若 ,则数列
,则数列 的通项公式为 ( )
的通项公式为 ( )
A. | B.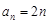 | C. | D.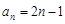 |
等差数列前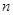 项和为
项和为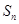 ,若
,若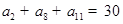 ,则
,则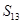 的值是( )
的值是( )
| A. 130 | B. 65 | C. 70 | D. 75 |
等差数列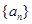 的前
的前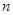 项和为
项和为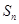 ,且
,且 ,则公差
,则公差 等于( )
等于( )
A.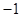 | B.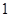 | C. | D. |
已知 为等差数列,其公差为-2,且
为等差数列,其公差为-2,且 是
是 与
与 的等比中项,
的等比中项, 为
为 前
前 项和,
项和, 则
则 的值为( )
的值为( )
| A.-110 | B.-90 | C.90 | D.110 |
如果等差数列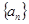 中,
中, ,那么
,那么 等于( )
等于( )
| A.21 | B.30 | C.35 | D.40 |
已知数列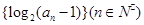 是等差数列,且
是等差数列,且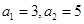 ,则
,则 ( )
( )
| A.2 | B.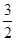 | C.1 | D.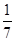 |
已知数列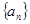 是等差数列,且
是等差数列,且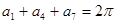 ,则
,则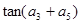 的值为( )
的值为( )
A.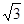 | B.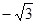 | C.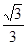 | D.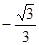 |
已知首项为正数的等差数列{an}的前n项和为Sn,若a1 006和a1 007是方程x2-2 012x-2 011=0的两根,则使Sn>0成立的正整数n的最大值是( ).
| A.1006 | B.1007 | C.2011 | D.2012 |