题目内容
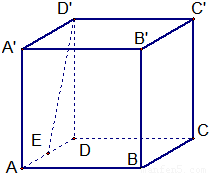
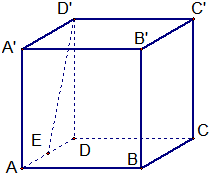 如图,ABCD-A′B′C′D′是棱长为2的正方体,E是棱AD的中点.
如图,ABCD-A′B′C′D′是棱长为2的正方体,E是棱AD的中点.
(1)求证:异面直线D′E⊥CD;
(2)求异面直线AC,BC′所成的角的大小;
(3)求三棱锥B′-A′BC′的表面积.
解:(1)ABCD-A′B′C′D′是棱长为2的正方体
∴CD⊥面A'D'DA
而D'E?面A'D'DA
∴异面直线D′E⊥CD
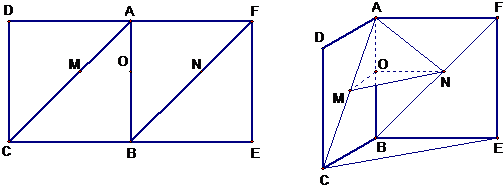
(2)将BC′平移到至AD',连接CD'
∴∠D′AC为异面直线AC,BC′所成的角,
而AD′=D′C=AC
∴∠D′AC=60°
(3)三棱锥B′-A′BC′的表面是由三个直角三角形和一个等边三角形组成
∴三棱锥B′-A′BC′的表面积为3× ×2×2+
×2×2+ =6+2
=6+2
分析:(1)ABCD-A′B′C′D′是棱长为2的正方体,根据线面垂直的性质定理可知D′E⊥CD;
(2)将BC′平移到至AD',连接CD',则∠D′AC为异面直线AC,BC′所成的角,而三角形AD′C为等边三角形,从而求出所求;
(3)三棱锥B′-A′BC′的表面是由三个直角三角形和一个等边三角形组成,然后求所各个面的面积
点评:本题主要考查了异面直线所成角和三棱锥表面积的度量,同时考查了空间想象能力,属于中档题.

∴CD⊥面A'D'DA
而D'E?面A'D'DA
∴异面直线D′E⊥CD
(2)将BC′平移到至AD',连接CD'
∴∠D′AC为异面直线AC,BC′所成的角,
而AD′=D′C=AC
∴∠D′AC=60°
(3)三棱锥B′-A′BC′的表面是由三个直角三角形和一个等边三角形组成
∴三棱锥B′-A′BC′的表面积为3×
 ×2×2+
×2×2+ =6+2
=6+2
分析:(1)ABCD-A′B′C′D′是棱长为2的正方体,根据线面垂直的性质定理可知D′E⊥CD;
(2)将BC′平移到至AD',连接CD',则∠D′AC为异面直线AC,BC′所成的角,而三角形AD′C为等边三角形,从而求出所求;
(3)三棱锥B′-A′BC′的表面是由三个直角三角形和一个等边三角形组成,然后求所各个面的面积
点评:本题主要考查了异面直线所成角和三棱锥表面积的度量,同时考查了空间想象能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,ABCD是菱形,PA⊥平面ABCD,PA=AD=2,∠BAD=60°.
如图,ABCD是菱形,PA⊥平面ABCD,PA=AD=2,∠BAD=60°.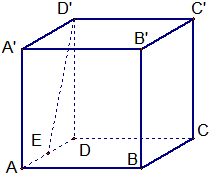 如图,ABCD-A′B′C′D′是棱长为2的正方体,E是棱AD的中点.
如图,ABCD-A′B′C′D′是棱长为2的正方体,E是棱AD的中点.