Question

【题目】如图，四边形是边长为4的正方形，点为边上任意一点（与点不重合），连接，过点作交于点，且，过点作，交于点，连接，设.

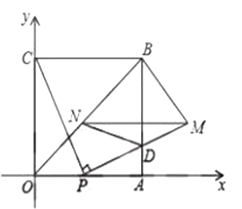
（1）求点的坐标（用含的代数式表示）

（2）试判断线段的长度是否随点的位置的变化而改变？并说明理由.

（3）当为何值时，四边形的面积最小.

（4）在轴正半轴上存在点，使得是等腰三角形，请直接写出不少于4个符合条件的点的坐标（用含的式子表示）

Answer 1

【答案】（1）（2）的长度不变（3）（4） ， ，

【解析】【试题分析】（1）作于点，依据，及，推得，即，进而依据，推得，借助，推出≌（），求出， ，则

进而求出点的坐标为；（2）借助，点，求出直线的解析式为： ，然后再依据点在直线上，且，求得，进而得到点，从而求出，即的长度不变；（3）借助（1）的结论，及，推得∽，故，从而求得， ， ，建立函数，求出当时，四边形的面积最小，最小值6；（4）借助图形的直观可以探求出在轴正半轴上存在点，使得是等腰三角形，此时点的坐标为： ， ， ， ：

解：（1）作于点，∴，

∵，∴，∴，

又∵，∴，∵，

∴≌（）

∴， ，∴

∴点的坐标为.

（2）线段长度不变.

∵，点，∴直线的解析式为： ，

∵点在直线上，且， ，∴点

∴，即的长度不变.

（3）由（1）知， ，又∵

∴∽，∴，

∵， ，∴

∴，得，

∴

∵， ，

∴

∴当时，四边形的面积最小，最小值6；

（4）在轴正半轴上存在点，使得是等腰三角形，此时点的坐标为： ， ， ，