题目内容
设数列{an}的前n项和为Sn，对任意的正整数n，都有an=5Sn+1成立，记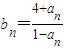
（n∈N*），（1）求数列{bn}的通项公式；
（2）记Cn=b2n-b2n-1（n∈N*），设数列{Cn}的前n和为Tn，求证：对任意正整数n，都有
．
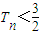【答案】分析：（1）令n等于1代入an=5Sn+1中，即可求出首项a1，然后把n换为n+1，利用an=5Sn+1表示出
，它的值即为公比，得到此数列为等比数列，然后根据首项和公比写出数列的通项公式即可，因而可得出bn的通项公式；
（2）根据bn的通项公式，计算出cn的通项公式，再比较Tn与
的大小；
解答：解：（1）∵5Sn=an-1
当n=1时，a1=5a1+1∴
当n≥2时，5an=5Sn-5Sn-1=an-1-（an-1-1）=an-an-1，
∴数列{an}成等比数列，其首项
，公比
∴
∴
（n∈N*） （5分）
（2）由（1）知
∴
=
又 b1=3，
∴
当n=1时，
当n≥2时，
（12分）
点评：此题考查学生灵活运用等比数列的通项公式及前n项和的公式化简求出，会确定一个数列为等比数列，考查数列递推式的求解及相关计算．是一道综合题．
，它的值即为公比，得到此数列为等比数列，然后根据首项和公比写出数列的通项公式即可，因而可得出bn的通项公式；（2）根据bn的通项公式，计算出cn的通项公式，再比较Tn与
的大小；解答：解：（1）∵5Sn=an-1
当n=1时，a1=5a1+1∴
当n≥2时，5an=5Sn-5Sn-1=an-1-（an-1-1）=an-an-1，
∴数列{an}成等比数列，其首项
，公比∴
∴（n∈N*） （5分）（2）由（1）知
∴
=又 b1=3，
∴当n=1时，
当n≥2时，
（12分）点评：此题考查学生灵活运用等比数列的通项公式及前n项和的公式化简求出，会确定一个数列为等比数列，考查数列递推式的求解及相关计算．是一道综合题．
练习册系列答案
相关题目