题目内容
已知a∈R,函数f(x)=(-x2+ax)ex(x∈R,e为自然对数的底数).
(Ⅰ)当a=2时,求函数f(x)的单调递增区间;
(Ⅱ)若函数f(x)在(-1,1)上单调递增,求a的取值范围.
解:(Ⅰ)当a=2时,f(x)=(-x2+2x)ex,f′(x)=-(x2-2)ex
令f′(x)>0,得x2-2<0,∴- <x<
<x<
∴f(x)的单调递增区间是(- ,
, );
);
(Ⅱ)f′(x)=[-x2+(a-2)x+a]ex,若f(x)在(-1,1)内单调递增,即当-1<x<1时,f′(x)≥0,
即-x2+(a-2)x+a≥0对x∈(-1,1)恒成立,
即a≥ 对x∈(-1,1)恒成立,
对x∈(-1,1)恒成立,
令y= ,则y′=
,则y′=
∴y= 在(-1,1)上单调递增,∴y<1+1-
在(-1,1)上单调递增,∴y<1+1-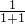 =
=
∴
当a= 时,当且仅当x=0时,f′(x)=0
时,当且仅当x=0时,f′(x)=0
∴a的取值范围是[ ,+∞).
,+∞).
分析:(Ⅰ)求导函数,令f′(x)>0,可得f(x)的单调递增区间;
(Ⅱ)f′(x)=[-x2+(a-2)x+a]ex,若f(x)在(-1,1)内单调递增,即当-1<x<1时,f′(x)≥0,即-x2+(a-2)x+a≥0对x∈(-1,1)恒成立,分离参数求最值,即可求a的取值范围.
点评:本题考查导数知识的运用,考查函数的单调性,考查学生分析解决问题的能力,属于中档题.
令f′(x)>0,得x2-2<0,∴-
 <x<
<x<
∴f(x)的单调递增区间是(-
 ,
, );
);(Ⅱ)f′(x)=[-x2+(a-2)x+a]ex,若f(x)在(-1,1)内单调递增,即当-1<x<1时,f′(x)≥0,
即-x2+(a-2)x+a≥0对x∈(-1,1)恒成立,
即a≥
 对x∈(-1,1)恒成立,
对x∈(-1,1)恒成立,令y=
 ,则y′=
,则y′=
∴y=
 在(-1,1)上单调递增,∴y<1+1-
在(-1,1)上单调递增,∴y<1+1-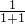 =
=
∴

当a=
 时,当且仅当x=0时,f′(x)=0
时,当且仅当x=0时,f′(x)=0∴a的取值范围是[
 ,+∞).
,+∞).分析:(Ⅰ)求导函数,令f′(x)>0,可得f(x)的单调递增区间;
(Ⅱ)f′(x)=[-x2+(a-2)x+a]ex,若f(x)在(-1,1)内单调递增,即当-1<x<1时,f′(x)≥0,即-x2+(a-2)x+a≥0对x∈(-1,1)恒成立,分离参数求最值,即可求a的取值范围.
点评:本题考查导数知识的运用,考查函数的单调性,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目