题目内容
已知定义域为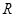 的函数
的函数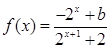 是奇函数.
是奇函数.
(Ⅰ)求实数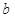 的值;
的值;
(Ⅱ)判断函数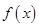 的单调性;
的单调性;
(Ⅲ)若对任意的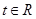 ,不等式
,不等式 恒成立,求
恒成立,求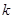 的取值范围.
的取值范围.
(Ⅰ)
(Ⅱ) 在
在 上为减函数。
上为减函数。
(Ⅲ)
解析试题分析:(Ⅰ)因为 是奇函数,所以
是奇函数,所以 =0,
=0,
即
(Ⅱ)由(Ⅰ)知 ,
,
设
 则
则
因为函数y=2 在R上是增函数且
在R上是增函数且 ∴
∴ >0
>0
又 >0 ∴
>0 ∴ >0即
>0即
∴ 在
在 上为减函数。
上为减函数。
(Ⅲ)因 是奇函数,从而不等式:
是奇函数,从而不等式: 
等价于 ,
,
因 为减函数,由上式推得:
为减函数,由上式推得: .即对一切
.即对一切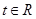 有:
有: ,
,
从而判别式
考点:函数的奇偶性、单调性,抽象不等式的解法。
点评:中档题,本题将函数的奇偶性、单调性,抽象不等式的解法综合在一起考查,注重了学生综合运用数学知识处理问题能力的考查。解答过程中,注意利用转化与化归思想,将抽象不等式问题,转化成具体不等式求解,是正确解题的关键。

练习册系列答案
相关题目
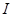 的函数
的函数 ,如果存在区间
,如果存在区间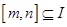 ,同时满足:
,同时满足: 在
在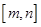 内是单调函数;②当定义域是
内是单调函数;②当定义域是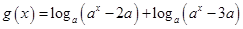 (其中
(其中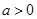 且
且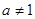 ),判断
),判断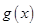 是否存在“好区间”,并
是否存在“好区间”,并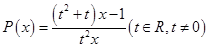 有“好区间”
有“好区间”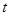 变化时,求
变化时,求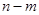 的最大值.
的最大值. +2bx+c,若a+b+c=0,且F(0)>0,F(1)>0.
+2bx+c,若a+b+c=0,且F(0)>0,F(1)>0. <—1.
<—1. ,
, ,
, 为奇函数,求
为奇函数,求 的值;
的值; 上是减函数;
上是减函数; 上的最小值.
上的最小值.  内单调递减,q:曲线y=x2+(2a-3)x+1与x轴交于不同的两点.如果p与q有且只有一个正确,求a的取值范围
内单调递减,q:曲线y=x2+(2a-3)x+1与x轴交于不同的两点.如果p与q有且只有一个正确,求a的取值范围 ,其中
,其中 ,区间
,区间 .
. 的长度(注:区间
的长度(注:区间 的长度定义为
的长度定义为 ;
; ,当
,当 时,求
时,求 (
( 为常数),且
为常数),且 在点
在点 处的切线平行于
处的切线平行于 轴.
轴.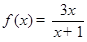 ,求
,求 在区间[2,5]上的最大值和最小值
在区间[2,5]上的最大值和最小值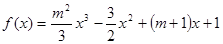
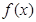 在
在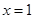 处取得极大值,求函数
处取得极大值,求函数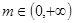 ,不等式
,不等式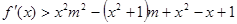 恒成立,求
恒成立,求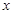 的取值范围
的取值范围