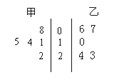
题目内容
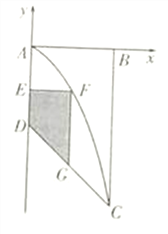
【题目】现有一块大型的广告宣传版面,其形状是右图所示的直角梯形![]() .某厂家因产品宣传的需要,拟投资规划出一块区域(图中阴影部分)为产品做广告,形状为直角梯形
.某厂家因产品宣传的需要,拟投资规划出一块区域(图中阴影部分)为产品做广告,形状为直角梯形![]() (点
(点![]() 在曲线段
在曲线段![]() 上,点
上,点![]() 在线段
在线段![]() 上).已知
上).已知![]() ,
, ![]() ,其中曲线段
,其中曲线段![]() 是以
是以![]() 为顶点,
为顶点, ![]() 为对称轴的抛物线的一部分.
为对称轴的抛物线的一部分.
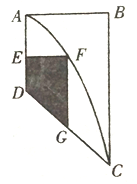
(1)建立适当的平面直角坐标系,分别求出曲线段![]() 与线段
与线段![]() 的方程;
的方程;
(2)求该厂家广告区域![]() 的最大面积.
的最大面积.
【答案】(1)直角坐标系见解析; 曲线段![]() 的方程为:
的方程为: ![]() ;
;
线段![]() 的方程为:
的方程为: ![]() .
.
(2) ![]() .
.
【解析】试题分析:(1)以AB为x轴,DA为y轴建立平面直角坐标系,则A(0,0),B(6,0),C(6,-12),D(0,-6).设曲线AC的方程x2=-2py,(p>0,0≤x≤6).代入C坐标即可求得p,即可求出曲线段![]() 的方程,由DC两点坐标即可求出线段
的方程,由DC两点坐标即可求出线段![]() 的方程;
的方程;
(2)设出F点横坐标a,将厂家广告区域![]() 的面积表示为a的函数,求出函数的最大值即可.
的面积表示为a的函数,求出函数的最大值即可.
试题解析:(1)以直线![]() 为
为![]() 轴,直线
轴,直线![]() 为
为![]() 轴建立平面直角坐标系(如图所示).
轴建立平面直角坐标系(如图所示).
则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
曲线段![]() 的方程为:
的方程为: ![]() ;
;
线段![]() 的方程为:
的方程为: ![]() ;
;
(2)设点![]() ,则需
,则需![]() ,即
,即![]() ,
,
则![]() ,
, ![]() ,
, ![]() .
.
∴![]() ,
, ![]() ,
, ![]() ,
,
则厂家广告区域![]() 的面积
的面积
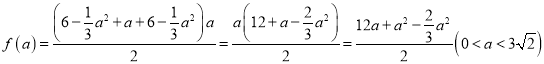 ,
,
∴![]() ,
,
令![]() ,得
,得![]() ,
, ![]() .
.
∴![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数.
上是减函数.
∴![]() .
.
∴厂家广告区域![]() 的面积最大值是
的面积最大值是![]() .
.
点睛:本题利用已知函数模型解决实际问题,关键是合理建系设出点坐标即可表示出面积的表达式,利用导数研究单调性即可求出最值.

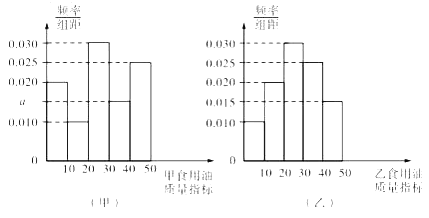
【题目】对某校高三年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表如下,频率分布直方图如图:
分组 | 频数 | 频率 |
[10,15) | 10 | 0.25 |
[15,20) | 24 | n |
[20,25) | m | p |
[25,30) | 2 | 0.05 |
合计 | M | 1 |

(1)求出表中M,p及图中a的值;
(2)若该校高三学生有240人,试估计该校高三学生参加社区服务的次数在区间[10,15)内的人数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间[25,30)内的概率.
【题目】2018年7月24日,长春长生生物科技有限责任公司先被查出狂犬病疫苗生产记录造假,因此,疫苗在上市前必须经过严格的检测,以保证疫苗使用的安全和有效.某生物制品研究所将某一型号疫苗用在动物小白鼠身上进行科研和临床实验,得到统计数据如表:现从所有试验小白鼠中任取一只,取到“注射疫苗”小白鼠的概率为![]() .
.
未感染病毒 | 感染病毒 | 总计 | |
未注射疫苗 | 20 | x | A |
注射疫苗 | 30 | y | B |
总计 | 50 | 50 | 100 |
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
(1)求2×2列联表中的数据![]() 的值;
的值;
(2)能否有99.9%把握认为注射此种疫苗有效?
附:![]() ,n=a+b+c+d.
,n=a+b+c+d.