题目内容
已知x、y∈[-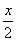 求cos(
求cos(
解:由已知得x3+sinx=2a=(-2y)3+sin(-2y),
若设f(t)=t3+sint,则f(x)=f(-2y).
而函数f(t)=t3+sint在[-![]() ,
,![]() ]上是递增函数(可用导数判断),
]上是递增函数(可用导数判断),
∴x=-2y,即![]() +y=0.故cos(
+y=0.故cos(![]() +y)=1.
+y)=1.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
题目内容
已知x、y∈[-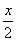 求cos(
求cos(
解:由已知得x3+sinx=2a=(-2y)3+sin(-2y),
若设f(t)=t3+sint,则f(x)=f(-2y).
而函数f(t)=t3+sint在[-![]() ,
,![]() ]上是递增函数(可用导数判断),
]上是递增函数(可用导数判断),
∴x=-2y,即![]() +y=0.故cos(
+y=0.故cos(![]() +y)=1.
+y)=1.

 导学全程练创优训练系列答案
导学全程练创优训练系列答案