题目内容
15、（几何证明选讲选做题）已知圆的直径AB=13，C为圆上一点，过C作CD⊥AB于D（AD＞BD），若CD=6，则AD的长为
9
．分析：已知中弦CD⊥AB于点D，AB为圆O的直径，由垂径定理，我们易得CD=ED，进而由相交弦定理，得CD2=AD•BD，由AB=13，CD=6，代入构造关于AD的方程，解方程即可得到AD的长．
解答：
解：延长CD交圆于另一E，如下图所示：
∵CD⊥AB，AB为圆的直径，
∴CD=DE=6
由相交弦定理可得
AD•BD=CD•ED
又由AB=13
∴AD•（13-AD）=36
解得AD=9，或AD=4（舍去）
故答案为：9
解：延长CD交圆于另一E，如下图所示：∵CD⊥AB，AB为圆的直径，
∴CD=DE=6
由相交弦定理可得
AD•BD=CD•ED
又由AB=13
∴AD•（13-AD）=36
解得AD=9，或AD=4（舍去）
故答案为：9
点评：本题考查的知识点是相交弦定理，垂径定理，其中解出AD的值有两个，要根据AD＞BD舍去一个，是本题的易忽略点．
练习册系列答案
相关题目
（几何证明选讲选做题）
（几何证明选讲选做题）如图，四边形ABCD内接于⊙O，AB为⊙O的直径，直线MN切⊙O于D，∠MDA=60°，则∠BCD=
（考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评分）
（几何证明选讲选做题）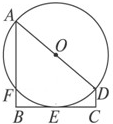
（几何证明选讲选做题）