题目内容
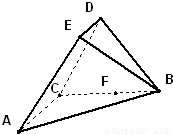
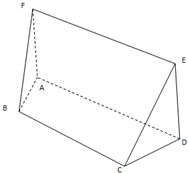 如图,在五面体ABCDEF中,四边形ADEF是正方形,FA⊥平面ABCD,BC‖AD,CD=1,AD=2
如图,在五面体ABCDEF中,四边形ADEF是正方形,FA⊥平面ABCD,BC‖AD,CD=1,AD=2| 2 |
(1)求异面直线CE与AF所成角的余弦值
(2)证明:CD⊥平面ABF.
分析:(1)通过平移,将FA平移到ED,可得∠CED为异面直线CE与AF所成的角.然后在Rt△CDE中,用余弦的定义加以计算,即可求出求出CE与AF所成角的余弦值.
(2)过点B作BG∥CD,交AD于点G,结合已知条件证出BG⊥AB,从而得出CD⊥AB.再由FA⊥平面ABCD,得CD⊥FA,利用线面垂直的判定定理,即可证出CD⊥平面ABF.
(2)过点B作BG∥CD,交AD于点G,结合已知条件证出BG⊥AB,从而得出CD⊥AB.再由FA⊥平面ABCD,得CD⊥FA,利用线面垂直的判定定理,即可证出CD⊥平面ABF.
解答:解:(1)∵四边形ADEF是正方形,所以FA∥ED.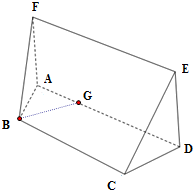
∴∠CED为异面直线CE与AF所成的角.
∵FA⊥平面ABCD,CD?平面ABCD,∴FA⊥CD,可得ED⊥CD.
∵在Rt△CDE中,CD=1,ED=2
,
∴CE=
=3,可得cos∠CED=
=
.
即异面直线CE和AF所成角的余弦值为
;
(Ⅱ)过点B作BG∥CD,交AD于点G,
∵BG∥CD,∴∠BGA=∠CDA=45°.
∵∠BAD=∠CDA=45°,
∴∠BGA+∠BAG=90°,可得BG⊥AB,
∵BG∥CD,∴CD⊥AB,
又∵FA⊥平面ABCD,CD?平面ABCD,
∴CD⊥FA,
∵FA、AB是平面ABF内的相交直线,
∴CD⊥平面ABF

∴∠CED为异面直线CE与AF所成的角.
∵FA⊥平面ABCD,CD?平面ABCD,∴FA⊥CD,可得ED⊥CD.
∵在Rt△CDE中,CD=1,ED=2
| 2 |
∴CE=
| CD2+ED2 |
| ED |
| EC |
2
| ||
| 3 |
即异面直线CE和AF所成角的余弦值为
2
| ||
| 3 |
(Ⅱ)过点B作BG∥CD,交AD于点G,
∵BG∥CD,∴∠BGA=∠CDA=45°.
∵∠BAD=∠CDA=45°,
∴∠BGA+∠BAG=90°,可得BG⊥AB,
∵BG∥CD,∴CD⊥AB,
又∵FA⊥平面ABCD,CD?平面ABCD,
∴CD⊥FA,
∵FA、AB是平面ABF内的相交直线,
∴CD⊥平面ABF
点评:本题在特殊多面体中证明线面垂直,并求异面直线所成角的大小.着重考查了空间线面垂直的判定与性质、异面直线的定义及其求法等知识,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
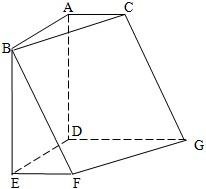 如图,在六面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,AB⊥AC,ED⊥DG,EF∥DG.且AB=AD=DE=DG=2,AC=EF=1.
如图,在六面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,AB⊥AC,ED⊥DG,EF∥DG.且AB=AD=DE=DG=2,AC=EF=1. 如图,在五面体ABCDE中,平面BCD⊥平面ABC,DC=DB=
如图,在五面体ABCDE中,平面BCD⊥平面ABC,DC=DB=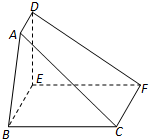 如图,在五面体ABC-DEF中,四边形BCFE 是矩形,DE⊥平面BCFE.
如图,在五面体ABC-DEF中,四边形BCFE 是矩形,DE⊥平面BCFE. ,AC=BC=2ED=2,AC⊥BC,且ED∥AC
,AC=BC=2ED=2,AC⊥BC,且ED∥AC  ,求二面角F-AE-B的余弦值.
,求二面角F-AE-B的余弦值.