题目内容
如图所示棱锥P—ABCD中,底面ABCD是正方形,边长为a,PD=a,PA=PC=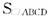
(1)在这个四棱锥中放入一个球,求球的最大半径;
(2)求四棱锥外接球的半径.
【探究】 (1)当所放的球与四棱锥各面都相切时球的半径最大,即球心到各个面的距离均相等,联想到用体积法求解.(2)四棱锥的外接球的球心到P、A、B、C、D五点的距离均为半径,只要找出球心的位置即可.在Rt△PDB中,斜边PB的中点为F,则PF=FB=FD,只要证明FA=FC=FP即可.
解:(1)设此球半径为R,最大的球应与四棱锥各个面都相切,设球心为S,连结SA、SB、SC、SD、SP,则把此四棱锥分为五个棱锥,设它们的高均为R.
VP—ABCD=![]() ·SABCD·PD=
·SABCD·PD=![]() ·a·a·a=
·a·a·a=![]() a3,
a3,
S△PAD=S△PDC=![]() ·a·a=
·a·a=![]() a2,
a2,
S△PAB=S△PBC=![]() ·a·
·a·![]() =
=![]() ,
,
![]() =a2.
=a2.
VP—ABCD=VS—PDA+VS—PDC+VS—ABCD+VS—PAB+VS—PBC,
![]() R(S△PAD+S△PDC+S△PAB+S△PBC+SABCD),
R(S△PAD+S△PDC+S△PAB+S△PBC+SABCD),
![]()
所以![]() ,
,
![]() ,
,
即球的最大半径为![]() .
.
(2)设PB的中点为F.
因为在Rt△PDB中,FP=FB=FD,
在Rt△PAB中,FA=FP=FB,
在Rt△PBC中,FP=FB=FC,
所以FP=FB=FA=FC=FD.
所以F为四棱锥外接球的球心,
则FP为外接球的半径.
因为FB=![]() PB,所以FB=
PB,所以FB=![]() .
.
所以四棱锥外接球的半径为![]() .
.
【规律总结】 (1)“内切”和“外接”等有关问题,首先要弄清几何体之间的相互关系,主要是指特殊的点、线、面之间的关系,然后把相关的元素放到这些关系中解决问题,例如本例中球内切于四棱锥时,球与四棱锥的五个面相切,即球心到五个面的距离相等.
(2)求体积或运用体积解决问题时,经常使用等积变换,即把一个几何体割补成其他几个几何体的和或差.

练习册系列答案
相关题目
 如图所示,四棱锥P-ABCD的底面为直角梯形,∠ADC=∠DCB=90°,AD=1,BC=3,PC=CD=2,PC⊥底面ABCD,E为AB的中点.
如图所示,四棱锥P-ABCD的底面为直角梯形,∠ADC=∠DCB=90°,AD=1,BC=3,PC=CD=2,PC⊥底面ABCD,E为AB的中点. (2012•广东)如图所示,在四棱锥P-ABCD中,AB⊥平面PAD,AB∥CD,PD=AD,E是PB的中点,F是CD上的点且
(2012•广东)如图所示,在四棱锥P-ABCD中,AB⊥平面PAD,AB∥CD,PD=AD,E是PB的中点,F是CD上的点且 (2010•武清区一模)如图所示,在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°AB=PA=2,PA⊥平面ABCD,E是PC的中点,F是AB的中点.
(2010•武清区一模)如图所示,在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°AB=PA=2,PA⊥平面ABCD,E是PC的中点,F是AB的中点.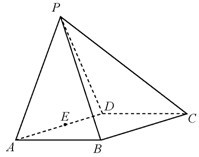 (2013•哈尔滨一模)如图所示,在四棱锥P-ABCD中,四边形ABCD为菱形,△PAD为等边三角形,平面 PAD⊥平面ABCD,∠DAB=60°,AB=2且,E为AD 的中点.
(2013•哈尔滨一模)如图所示,在四棱锥P-ABCD中,四边形ABCD为菱形,△PAD为等边三角形,平面 PAD⊥平面ABCD,∠DAB=60°,AB=2且,E为AD 的中点. (2009•滨州一模)如图所示,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,平面PBC⊥底面ABCD,且
(2009•滨州一模)如图所示,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,平面PBC⊥底面ABCD,且