Question

（2012•邯郸一模）在区间[-1，1]上任取两数s和t，则关于x的方程x²+2sx+t=0的两根都是正数的概率为（　　）

• A．

  1

  24

• B．

  1

  12

• C．

  1

  4

• D．

  1

  3

Answer 1

分析：先将二次方程x²+2sx+t=0的两根都是正数的s，t必须满足的条件列出来，再在坐标系sot中画出区域，最后求出面积比即可．

解答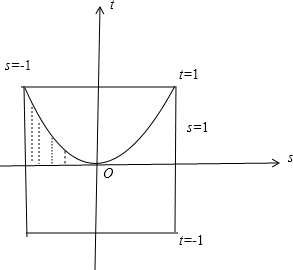：解：由题意可得，

-1≤s≤1 -1≤t≤1

，其区域是边长为2的正方形，面积为4
由二次方程x²+2sx+t=0有两正根可得

4s2-4t≥0 -2s＞0 t＞0

，其区域如图所示
即

s2≥t s＜0 t＞0

其区域如图所示，面积S=

∫

0 -1

s²ds=

1

3

s3

|

0 -1

=

1

3

所求概率P=

1 3

4

=

1

12

故选B

点评：本题主要考查了与面积有关的几何概率的求解，解题的关键是利用积分求出指定事件的面积