已知定圆⊙O的半径为r.A是圆内的一定点.OA=$\frac{r}{2}$.OB是⊙O的任一半径.作AP⊥OB交OB或OB的延长线于P.求P点的轨迹方程．题目和参考答案——青夏教育精英家教网——

题目内容

19．已知定圆⊙O的半径为r，A是圆内的一定点，OA=$\frac{r}{2}$，OB是⊙O的任一半径，作AP⊥OB交OB或OB的延长线于P，求P点的轨迹方程．

分析确定⊙O的方程，P的轨迹是以OA为直径的圆，即可求出P点的轨迹方程．

解答解：由题意，⊙O的方程为x²+y²=r²，A（$\frac{r}{2}$，0），
∵作AP⊥OB交OB或OB的延长线于P，
∴P的轨迹是以OA为直径的圆，方程为（x-$\frac{r}{4}$）²+y²=$\frac{1}{16}$r²．

点评本题考查圆的方程，考查代入法的运用，考查学生的计算能力，比较基础．

练习册系列答案

课课优能力培优100分系列答案

期末迎考特训系列答案

高效课时100系列答案

小学生百分易卷系列答案

帮你学系列答案

一卷通关系列答案

优百分课时互动系列答案

金牌夺冠一卷OK系列答案

核心360小学生赢在100系列答案

期末闯关100分系列答案

相关题目

9．若动点P在直线l₁：x-y+1=0上，动点Q在直线l₂：x+y-7=0上，且|PQ|=2，设线段PQ的中点为M（x₀，y₀），则x₀²+y₀²的取值范围是[16，36]．

10．已知函数f（x）=$\frac{e^x}{x+a}$，（a＜3且a∈Z），且函数f（x）在区间（-1，0）上单调递增，定义在R上的函数g（x）=（x+b）（x²-8），且函数g（x）在x=1处的切线与直线x-y=0垂直．
（Ⅰ）求函数f（x）与函数g（x）的解析式；
（Ⅱ）已知函数F（x）=$\left\{\begin{array}{l}f（x）•g（x），x≠-2\\-4{e^{-2}}，x=-2\end{array}$，试问：是否存在实数a，b，其中[a，b]⊆（-∞，4]，使得函数F（x）的值域也为[a，b]？若能，请求出相应的a、b；若不能，请说明理由．

7．已知函数f（x）=$\sqrt{3}$sinxcosx-cos²x+1
（1）求函数f（x）的单调递增区间；
（2）若f（$\frac{θ}{2}$+$\frac{π}{12}$）=$\frac{5}{6}$，θ∈（0，$\frac{π}{2}$），求cos（θ+$\frac{π}{4}$）的值．

14．已知：$\frac{{A}_{n}^{3}}{6}$=n（n∈N^*），（2-x）ⁿ=a₀+a₁x+a₂x²+…+a_nxⁿ
求a₀-a₁+a₂-…+（-1）ⁿa${\;}_{n}^{\;}$的值．

4．已知函数f（x）的定义域为[0，1]，求下列函数的定义域：
（1）f（x²）；
（2）f（$\sqrt{x}$-1）

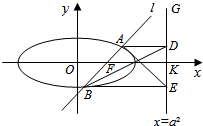如图，已知直线l：x=my+1过椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的右焦点F，且交椭圆C于A、B两点，点A、B在直线G：x=a²上的射影依次为点D、E．
（1）若抛物线x²=4$\sqrt{3}$y的焦点为椭圆的上顶点，求椭圆C的方程．
（2）若点N（$\frac{{a}^{2}+1}{2}$，0）为x轴上一点，求证：$\overrightarrow{AN}$=λ$\overrightarrow{NE}$．

8．在（1+x）ⁿ的展开式中，第9项为（　　）

C${\;}_{n}^{9}$x⁹

C${\;}_{n}^{8}$x⁸

C${\;}_{n}^{9}$x^n-9

C${\;}_{n}^{8}$x^n-8

9．已知某运动员每次投篮命中的概率都为40%．现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率：先由计算器算出0到9之间取整数值的随机数，用1，2，3，4表示命中，用5，6，7，8，9，0表示不命中；再以每三个随机数为一组，代表三次投篮的结果．经随机模拟产生了20组随机数：
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
据此估计，该运动员三次投篮恰有两次命中的概率为（　　）