题目内容
将圆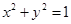 上每一点的横坐标保持不变,纵坐标变为原来的2倍,得曲线C.
上每一点的横坐标保持不变,纵坐标变为原来的2倍,得曲线C.
(1)写出C的参数方程;
(2)设直线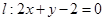 与C的交点为
与C的交点为 ,以坐标原点为极点,x轴正半轴为极坐标建立极坐标系,求过线段
,以坐标原点为极点,x轴正半轴为极坐标建立极坐标系,求过线段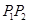 的中点且与
的中点且与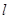 垂直的直线的极坐标方程.
垂直的直线的极坐标方程.
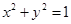 上每一点的横坐标保持不变,纵坐标变为原来的2倍,得曲线C.
上每一点的横坐标保持不变,纵坐标变为原来的2倍,得曲线C.(1)写出C的参数方程;
(2)设直线
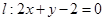 与C的交点为
与C的交点为 ,以坐标原点为极点,x轴正半轴为极坐标建立极坐标系,求过线段
,以坐标原点为极点,x轴正半轴为极坐标建立极坐标系,求过线段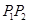 的中点且与
的中点且与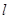 垂直的直线的极坐标方程.
垂直的直线的极坐标方程.(1)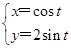 (t为参数);(2)
(t为参数);(2) 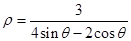 .
.
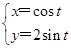 (t为参数);(2)
(t为参数);(2) 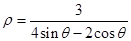 .
.试题分析:(1)设
 为圆上的点,在曲线C上任意取一点(x,y),再根据
为圆上的点,在曲线C上任意取一点(x,y),再根据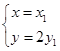 ,由于点
,由于点 在圆
在圆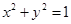 上,求出C的方程,化为参数方程.(2)解方程组求得
上,求出C的方程,化为参数方程.(2)解方程组求得 的坐标,可得线段
的坐标,可得线段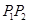 的中点坐标.再根据与l垂直的直线的斜率为
的中点坐标.再根据与l垂直的直线的斜率为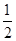 ,用点斜式求得所求的直线的方程,再根据
,用点斜式求得所求的直线的方程,再根据 可得所求的直线的极坐标方程.
可得所求的直线的极坐标方程.(1)设
 为圆上的点,在已知变换下位C上点(x,y),依题意,得
为圆上的点,在已知变换下位C上点(x,y),依题意,得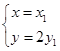 由
由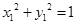 得
得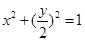 ,即曲线C的方程为
,即曲线C的方程为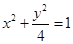 .,故C得参数方程为
.,故C得参数方程为 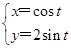 (t为参数).
(t为参数).(2)由
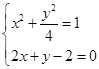 解得:
解得: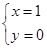 ,或
,或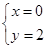 .
.不妨设
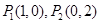 ,则线段
,则线段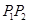 的中点坐标为
的中点坐标为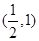 ,所求直线的斜率为
,所求直线的斜率为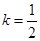 ,于是所求直线方程为
,于是所求直线方程为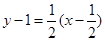 ,
,化极坐标方程,并整理得
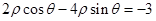 ,即
,即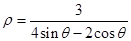 .
.
练习册系列答案
相关题目
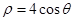 上的点到直线
上的点到直线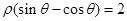 的最大距离为 .
的最大距离为 .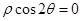 表示的曲线为( )
表示的曲线为( )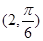 到直线
到直线 的距离是
的距离是 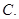
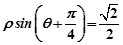 ,则点A(2,
,则点A(2,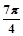 )到这条直线的距离为 .
)到这条直线的距离为 .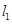 的方程是
的方程是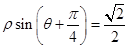 ,以极点为原
,以极点为原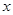 轴的正半轴建立直角坐标系,在直角坐标系中,直线
轴的正半轴建立直角坐标系,在直角坐标系中,直线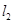 的方程是
的方程是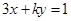 .如果直线
.如果直线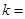 .
.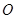 ,极轴与
,极轴与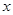 轴的非负半轴重合.若直线
轴的非负半轴重合.若直线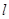 的极坐标方程为
的极坐标方程为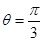
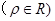 ,曲线
,曲线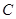 的参数方程为
的参数方程为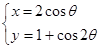
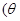 为参数,且
为参数,且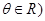 ,则直线
,则直线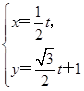 (t为参数),求直线l被曲线C截得的线段的长度.
(t为参数),求直线l被曲线C截得的线段的长度.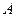 的坐标为
的坐标为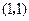 ,点
,点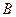 的坐标为
的坐标为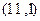 ,点
,点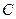 到直线
到直线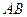 的距离为
的距离为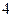 ,且
,且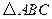 是直角三角形,则满足条件的点
是直角三角形,则满足条件的点