题目内容
进行直角坐标方程与极坐标方程的互化.(1)y2=4x;(2)y2+x2-2x-1=0;(3)θ=![]() ;
;
(4)ρcos2![]() =1;(5)ρ2cos(2θ)=4;(6)ρ=
=1;(5)ρ2cos(2θ)=4;(6)ρ=![]() .
.
思路分析:极坐标系和直角坐标系都是用一对有序实数来确定平面上一点的位置的方法.在解这类题时,除正确使用互化公式外,还要注意与恒等变换等知识相结合.
解:(1)将x=ρcosθ,y=ρsinθ代入y2=4x,得(ρsinθ)2=4ρcosθ.
化简得ρsin2θ=4cosθ.
(2)将x=ρcosθ,y=ρsinθ代入y2+x2-2x-1=0,得(ρsinθ)2+(ρcosθ)2-2ρcosθ-1=0.
化简得ρ2-2ρcosθ-1=0.
(3)∵tanθ=![]() ,∴tan
,∴tan![]() =
=![]() =
=![]() .化简得y=
.化简得y=![]() x(x≥0).
x(x≥0).
(4)∵ρcos2![]() =1,
=1,
∴ρ·![]() =1,即ρ+ρcosθ=2.
=1,即ρ+ρcosθ=2.
∴![]() +x=2,化简得y2=-4(x-1).
+x=2,化简得y2=-4(x-1).
(5)∵ρ2cos(2θ)=4,∴ρ2cos2θ-ρ2sin2θ=4,即x2-y2=4.
(6)∵ρ=![]() ,∴2ρ-ρcosθ=1.
,∴2ρ-ρcosθ=1.
∴![]() =1,化简得3x2+4y2-2x-1=0.
=1,化简得3x2+4y2-2x-1=0.
方法归纳 在进行两种坐标间的互化时,要注意:
(1)互化公式是有三个前提条件的,极点与直角坐标系的原点重合;极轴与直角坐标系的横轴的正半轴重合;两种坐标系的单位长度相同.
(2)由直角坐标求极坐标时,理论上不是唯一的,但这里约定只在0≤θ<2π范围内求值.
(3)由直角坐标方程化为极坐标方程,最后要化简.
(4)由极坐标方程化为直角坐标方程时要注意变形的等价性,通常总要用ρ去乘方程的两端,应该检查极点是否在曲线上,若在,是等价变形,否则不是等价变形.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
 中,把矩阵
中,把矩阵 确定的压缩变换
确定的压缩变换 与矩阵
与矩阵 确定的旋转变换
确定的旋转变换 进行复合,得到复合变换
进行复合,得到复合变换 .
.
 在复合变换
在复合变换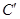 的方程.
的方程. 的参数方程为
的参数方程为 (
( 为参数),
为参数), 、
、 分别为直线
分别为直线 轴、
轴、 轴的交点,线段
轴的交点,线段 的中点为
的中点为 .
. 为极点,
为极点, 的极坐标方程.
的极坐标方程. 的解集与关于
的解集与关于 的解集相等.
的解集相等. ,
, 的值;
的值;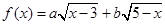 的最大值,以及取得最大值时
的最大值,以及取得最大值时 为极点,
为极点, 轴的正半轴为极轴。已知点
轴的正半轴为极轴。已知点 的直角坐标为(1,-5),点
的直角坐标为(1,-5),点 的极坐标为
的极坐标为 若直线
若直线 过点
过点 ,圆
,圆 以
以 为半径。
为半径。 先进行横坐标缩为原来的一半,纵坐标保持不变的伸缩变换,再做关于
先进行横坐标缩为原来的一半,纵坐标保持不变的伸缩变换,再做关于 对任意
对任意 无实根,求实数
无实根,求实数 的取值范围.
的取值范围.