题目内容
已知向量 =(sin2x,cos2x),
=(sin2x,cos2x), =(cos
=(cos ,sin
,sin ),函数f(x)=
),函数f(x)= +2a(其中a为实常数)
+2a(其中a为实常数)
(1)求函数f(x)的最小正周期;
(2)求函数f(x)的单调递减区间.
解:(1)f(x)= +2a=
+2a= (sin2x,cos2x)•(cos
(sin2x,cos2x)•(cos ,sin
,sin )
)
=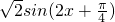
∴f(x)的最小正周期T=
(2)由2kπ+ ≤2x+
≤2x+ ≤
≤
得
∴f(x)的单调递减区间是:
分析:求出f(x)= +2a的表达式,化简为一个角的一个三角函数的形式,然后求其最小正周期,求其单调减区间.
+2a的表达式,化简为一个角的一个三角函数的形式,然后求其最小正周期,求其单调减区间.
点评:本题考查三角函数的周期性及其求法,向量数乘的运算及其几何意义,复合三角函数的单调性,考查计算能力,是中档题.
 +2a=
+2a= (sin2x,cos2x)•(cos
(sin2x,cos2x)•(cos ,sin
,sin )
)=
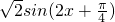
∴f(x)的最小正周期T=

(2)由2kπ+
 ≤2x+
≤2x+ ≤
≤
得

∴f(x)的单调递减区间是:

分析:求出f(x)=
 +2a的表达式,化简为一个角的一个三角函数的形式,然后求其最小正周期,求其单调减区间.
+2a的表达式,化简为一个角的一个三角函数的形式,然后求其最小正周期,求其单调减区间.点评:本题考查三角函数的周期性及其求法,向量数乘的运算及其几何意义,复合三角函数的单调性,考查计算能力,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目